5.递推是认识数列的重要手段，递推公式是确定数列的一种方式，根据数列的递推关系写出数列.

●点击双基

4.数列的分类

(1)按项分类

有穷数列:项数有限；无穷数列:项数无限.

(2)按a_n的增减性分类

递增数列：对于任何n∈N^*，均有a_n+1＞a_n；

递减数列：对于任何n∈N^*，均有a_n+1＜a_n；

摆动数列：例如:－1，1，－1，1，…；

常数数列：例如：6，6，6，6，…；

有界数列：存在正数M使|a_n|≤M，n∈N^*；

无界数列：对于任何正数M，总有项a_n使得|a_n|＞M.

3.数列的前n项和

数列{a_n}的前n项之和，叫做数列的前n项和，常用S_n表示.

S_n与通项a_n的基本关系是：

a_n=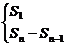　

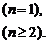
S_n=a₁+a₂+…+a_n.

2.通项公式

如果数列{a_n}的第n项a_n与项数n之间的函数关系可以用一个公式来表达，那么这个公式就叫做数列的通项公式，可以记为a_n=f(n).

并非每一个数列都可以写出通项公式，有些数列的通项公式也并非是唯一的.

1.数列：按一定次序排列的一列数叫做数列.

(1)数列的一般形式可以写成a₁，a₂，a₃，…，a_n，…，简记为{a_n}，其中a_n是数列的第n项.

(2)可视数列为特殊函数，它的定义域是正自然数集的子集(必须连续)，因此研究数列可联系函数的相关知识，如数列的表示法(列表法、图象法、公式法等)、数列的分类(有限和无穷、有界无界、单调或摆动等).应注意用函数的观点分析问题.

3.1　 数列的概念

●知识梳理

6.解题要善于总结基本数学方法.如观察法、类比法、错位相减法、待定系数法、归纳法、数形结合法，养成良好的学习习惯，定能达到事半功倍的效果.

5.深刻理解等差(比)数列的定义，能正确使用定义和等差(比)数列的性质是学好本章的关键.

4.等价转化是数学复习中常常运用的，数列也不例外.如a_n与S_n的转化；将一些数列转化成等差(比)数列来解决等.复习时，要及时总结归纳.

3.分类讨论的思想在本章尤为突出.学习时考虑问题要全面，如等比数列求和要注意q=1和q≠1两种情况等等.