
6.已知在正项数列{an}中,Sn表示前n项和且2 =an+1,求an.
=an+1,求an.
解:由已知2 =an+1,得当n=1时,a1=1;当n≥2时,an=Sn-Sn-1,代入已知有2
=an+1,得当n=1时,a1=1;当n≥2时,an=Sn-Sn-1,代入已知有2 =
=
Sn-Sn-1+1,即Sn-1=( -1)2.又an>0,故
-1)2.又an>0,故 =
= -1或
-1或 = 1-
= 1- (舍),即
(舍),即 -
- =1(n≥2),由定义得{
=1(n≥2),由定义得{ }是以1为首项,1为公差的等差数列,∴
}是以1为首项,1为公差的等差数列,∴ =n.故an=2n-1.
=n.故an=2n-1.
培养能力
5.已知数列{an}的前n项和Sn满足log2(Sn+1)=n+1,求数列{an}的通项公式.
解:由已知Sn+1=2n-1,得Sn=2n+1-1,故当n=1时,a1=S1=3;当n≥2时,an=Sn-Sn-1=2n,故an=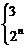
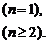
4.(2004年春季上海,8)根据下列5个图形及相应点的个数的变化规律,试猜测第n个图中有___________________个点.

解析:观察图中五个图形点的个数分别为1,1×2+1,2×3+1,3×4+1,4×5+1,故第n个图中个数为(n-1)×n+1=n2-n+1.
答案:n2-n+1
3.设{an}是正数组成的数列,其前n项和为Sn,并且对所有自然数n,an与2的等差中项等于Sn与2的等比中项,写出此数列的前三项:______________,______________,______________.
解析:由题意得 =
=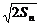 ,由此公式分别令n=1,n=2,n=3可依次解出前三项.
,由此公式分别令n=1,n=2,n=3可依次解出前三项.
答案:2 6 10
2.设an=-n2+10n+11,则数列{an}从首项到第______________项的和最大.
A.10 B.11 C.10或11 D.12
解析:an=-n2+10n+11是关于n的二项函数,它是抛物线f(x)=-x2+10x+11上的一些离散的点,从图象可看出前10项都是正数,第11项是0,所以前10项或前11项的和最大.
另解: 由-n2+10n+11≥0得-1≤n≤11,
又n∈N*,∴0<n≤11.∴前10项为正,第11项为0.
答案:C
1.若数列{an}前8项的值各异,且an+8=an对任意的n∈N*都成立,则下列数列中,能取遍数列{an}前8项值的数列是
A.{a2k+1} B.{a3k+1} C.{a4k+1} D.{a6k+1}
解析:由已知得数列以8为周期,当k分别取1,2,3,4,5,6,7,8时,a3k+1分别与数列中的第4项,第7项,第2项,第5项,第8项,第3项,第6项,第1项相等,故{a3k+1}能取遍前8项.
答案:B
4.已知an= ,且数列{an}共有100项,则此数列中最大项为第____________项,最小项为第___________________项.
,且数列{an}共有100项,则此数列中最大项为第____________项,最小项为第___________________项.
解析:an= =1+
=1+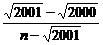 ,又44<
,又44<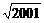 <45,
<45,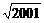 -
- >0,故第45项最大,第44项最小.
>0,故第45项最大,第44项最小.
答案:45 44
●典例剖析
[例1] 在数列{an}中,a1=1,an+1= ,求an.
,求an.
剖析:将递推关系式变形,观察其规律.
解:原式可化为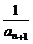 -
-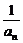 =n,
=n,
∴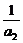 -
- =1,
=1, -
-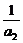 =2,
=2,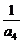 -
- =3,…,
=3,…,
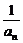 -
- =n-1.
=n-1.
相加得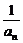 -
- =1+2+…+(n-1),
=1+2+…+(n-1),
∴an=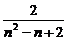 .
.
评析:求数列通项公式,特别是由递推公式给出数列时,除迭加、迭代、迭乘外还应注意变形式是否是等差(等比)数列.对于数列递推公式不要升温,只要能根据递推公式写出数列的前几项,由此来猜测归纳其构成规律.
[例2] 有一数列{an},a1=a,由递推公式an+1= ,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
剖析:可根据递推公式写出数列的前4项,然后分析每一项与该项的序号之间的关系,归纳概括出an与n之间的一般规律,从而作出猜想,写出满足前4项的该数列的一个通项公式.
解:∵a1=a,an+1= ,∴a2=
,∴a2= ,
,
a3= =
= =
= ,
,
a4= =
=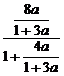 =
= .
.
观察规律:an=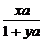 形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
∴an= .
.
评述:从特殊的事例,通过分析、归纳、抽象总结出一般规律,再进行科学地证明,这是创新意识的具体体现,这种探索问题的方法,在解数列的有关问题中经常用到,应引起足够的重视.
思考讨论
请同学总结解探索性问题的一般思路.
[例3] 已知数列{an}的通项公式an=cn+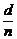 ,且a2=
,且a2= ,a4=
,a4= ,求a10.
,求a10.
剖析:要求a10,只需求出c、d即可.
解:由题意知 解得
解得
∴an= n+
n+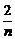 .∴a10=
.∴a10= ×10+
×10+ =
= .
.
评述:在解题过程中渗透了函数与方程的思想.
●闯关训练
夯实基础
3.根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn= (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是
A.5、6月 B.6、7月 C.7、8月 D.8、9月
解法一:由Sn解出an= (-n2+15n-9),再解不等式
(-n2+15n-9),再解不等式 (-n2+15n-9)>1.5,得6<n<9.
(-n2+15n-9)>1.5,得6<n<9.
解法二:将选项中的月份代入计算验证.
答案:C
2.已知数列{an}中,a1=1,a2=3,an=an-1+ (n≥3),则a5等于
(n≥3),则a5等于
A. B.
B. C.4 D.5
C.4 D.5
解析:令n=3,4,5,求a5即可.
答案:A
1.数列{an}中,a1=1,对于所有的n≥2,n∈N都有a1·a2·a3·…·an=n2,则a3+a5等于
A. B.
B. C.
C. D.
D.
解析一:令n=2、3、4、5,分别求出a3= ,a5=
,a5= ,∴a3+a5=
,∴a3+a5= .
.
解析二:当n≥2时,a1·a2·a3·…·an=n2.
当n≥3时,a1·a2·a3·…·an-1=(n-1)2.
两式相除an=( )2,
)2,
∴a3= ,a5=
,a5= .∴a3+a5=
.∴a3+a5= .
.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com