=－S_n+2S₆=n²－12n+72.

∴T_n=　

评述：此类求和问题先由a_n的正负去掉绝对值符号，然后分类讨论转化成{a_n}的求和问题.

深化拓展

若此题的S_n=n²－12n，那又该怎么求T_n呢？

答案：T_n=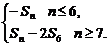

●闯关训练

夯实基础

1.等差数列{a_n}中，a₁₀＜0，a₁₁＞0且a₁₁＞|a₁₀|，S_n为其前n项和，则

A.S₁，S₂，…，S₁₀都小于0，S₁₁，S₁₂，…都大于0

B.S₁，S₂，…，S₁₉都小于0，S₂₀，S₂₁，…都大于0

C.S₁，S₂，…，S₅都小于0，S₆，S₇，…都大于0

D.S₁，S₂，…，S₂₀都小于0，S₂₁，S₂₂，…都大于0

解析：由题意知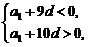

可得d＞0，a₁＜0.

又a₁₁＞|a₁₀|=－a₁₀，

∴a₁₀+a₁₁＞0.

由等差数列的性质知a₁+a₂₀=a₁₀+a₁₁＞0，

∴S₂₀=10(a₁+a₂₀)＞0.

答案：B

3.重视函数与数列的联系，重视方程思想在数列中的应用.

拓展题例

[例1] 已知f(x)=(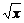+)²(x≥0)，又数列{a_n}(a_n＞0)中，a₁=2，这个数列的前n项和的公式S_n(n∈N^*)对所有大于1的自然数n都有S_n=f(S_n－1).

(1)求数列{a_n}的通项公式；

(2)若b_n=(n∈N^*)，求证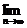(b₁+b₂+…+b_n－n)=1.

分析：由于已知条件给出的是S_n与S_n－1的函数关系，而要求的是a_n的通项公式，故关键是确定S_n.

解：(1)∵f(x)=(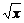+)²，

∴S_n=(+)².

∴－=.又=，

故有=+(n－1)=n，

即S_n=2n²(n∈N^*).

当n≥2时，a_n=S_n－S_n－1=2n²－2(n－1)²=4n－2；

当n=1时，a₁=2，适合a_n=4n－2.

因此，a_n=4n－2(n∈N^*).

(2)∵b_n==1+－，

∴b₁+b₂+b₃+…+b_n－n=1－.

从而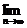(b₁+b₂+…+b_n－n)=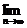(1－)=1.

[例2] 已知数列{a_n}中，a_n∈(0，)，a_n＝+·a_n－1²，其中n≥2，n∈N^*，求证：对一切自然数n都有a_n＜a_n+1成立.

证明：a_n+1－a_n＝+a_n²－a_n＝(a_n－1)²－.

∵0＜a_n＜，∴－1＜a_n－1＜－.

∴＜(a_n－1)²＜.

∴(a_n－1)²－＞0.

∴a_n+1－a_n＞0，即a_n＜a_n+1对一切自然数n都成立.

2.给出数列的方法中，递推关系包含两种：一种是项和项之间的关系；另一种是项和前n项和S_n之间的关系.要用转化的数学思想方法.转化是数学中最基本、最常用的解题策略，S_n和a_n的转化，可给出数列，问题总是在一步步的转化过程中得到解决，在运用转化的方法时，一定要围绕转化目标转化.

1.要注意强调数列、数列的项、数列的通项三个概念的区别.

3.求数列的通项公式是本节的重点，主要掌握两种求法.

(1)由数列的前几项归纳出一个通项公式，关键是善于观察.(2)数列{a_n}的前n项和S_n与数列{a_n}的通项公式a_n的关系，要注意验证能否统一到一个式子中.

●教师下载中心

教学点睛

2.对于符号(数字、字母、运算符号、关系符号)、图形、文字所表示的数学问题，要有目的地从局部到整体多角度进行观察，从而得出结论.

1.用归纳法依据前几项写出数列的一个通项公式，体现了由特殊到一般的思维方法，需要我们有一定的数学观察能力和分析能力，并熟知一些常见的数列的通项公式，如：数列{n²}，{2ⁿ}，{(－1)ⁿ}，{2n}，{2n－1}，并了解a_n=　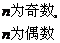 　的合一形式a_n=a+ b.

9.有一个细胞集合，在一小时里死亡两个，剩下的细胞每一个都分裂成两个，假设开始有10个细胞，问经过几个小时后，细胞的个数为1540个？

解：设n小时后的细胞个数为a_n，依题意得a_n+1=2(a_n－2)，所以a_n+1－4=2(a_n－4).

又∵a₁=10，∴a_n－4=(a₁－4)·2^n－1=3·2ⁿ.

∴a_n=3·2ⁿ+4，使3·2ⁿ+4=1540.

∴n=9.

●思悟小结

8.已知数列{a_n}的通项a_n=(n+1)()ⁿ(n∈N).试问该数列{a_n}有没有最大项？若有，求出最大项和最大项的项数；若没有，说明理由.

解：∵a_n+1－a_n

=(n+2)()ⁿ⁺¹－(n+1)()ⁿ

=()ⁿ·，

∴当n＜9时，a_n+1－a_n＞0，即a_n+1＞a_n；

当n=9时，a_n+1－a_n=0，即a_n+1=a_n；

当n＞9时，a_n+1－a_n＜0，即a_n+1＜a_n；

故a₁＜a₂＜a₃＜…＜a₉=a₁₀＞a₁₁＞a₁₂＞….

∴数列{a_n}有最大项a₉或a₁₀，其值为10·()⁹，其项数为9或10.

探究创新

7.(理)已知函数f(x)=－2x+2(≤x≤1)的反函数为y=g(x)，a₁=1，a₂=g(a₁)，a₃=g(a₂)，…，a_n=g(a_n－1)，…，求数列{a_n}的通项公式.

解：由已知得g(x)=－+1(0≤x≤1)，则a₁=1，a_n+1=－a_n+1.

令a_n+1－P=－(a_n－P)，则a_n+1=－a_n+P，比较系数得P=.

由定义知，数列{a_n－}是公比q=－的等比数列，则a_n－=(a₁－)·(－)^n－1=

［1－(－)ⁿ］.于是a_n=－(－)ⁿ.

(文)根据下面各数列的前几项，写出数列的一个通项公式：

(1)3，5，9，17，33，…；

(2)，，，，，…；

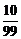(3)2，－6，12，－20，30，－42，….

解：(1)联想数列2，4，8，16，32，…，可知所求通项公式为a_n=2ⁿ+1.

(2)分别观察各项分子与分母的规律，分子为偶数列{2n}；分母为1×3，3×5，5×7，7×9，…，故所求通项公式为a_n=.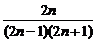

(3)将数列变形为1×2，－2×3，3×4，－4×5，…，于是可得已知数列的通项公式为a_n=(－1)ⁿ⁺¹·n(n+1).