8.设数列{a_n}、{b_n}(b_n＞0，n∈N^*)，满足a_n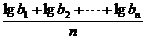＝(n∈N^*)，证明：{a_n}为等差数列的充要条件是{b_n}为等比数列.

证明：充分性：若{b_n}为等比数列，设公比为q，则a_n＝＝＝lgb₁+(n－1)lgq，a_n+1－a_n＝lgq为常数，

∴{a_n}为等差数列.

必要性：由a_n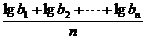＝得na_n＝lgb₁+lgb₂+…+lgb_n，(n+1)a_n+1＝lgb₁+lgb₂+…+lgb_n+1，

∴n(a_n+1－a_n)+a_n+1＝lgb_n+1.

若{a_n}为等差数列，设公差为d，

则nd+a₁+nd＝lgb_n+1，

∴b_n+1＝10，b_n＝10.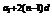

∴＝10^2d为常数.

∴{b_n}为等比数列.

探究创新

7.数列{a_n}的前n项和为S_n，数列{b_n}中，b₁=a₁，b_n=a_n－a_n－1(n≥2)，若a_n+S_n=n.

(1)设c_n=a_n－1，求证：数列{c_n}是等比数列；

(2)求数列{b_n}的通项公式.

(1)证明：∵a₁=S₁，a_n+S_n=n，∴a₁+S₁=1，得a₁=.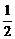

又a_n+1+S_n+1=n+1，两式相减得2(a_n+1－1)=a_n－1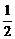，即=，也即=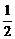，故数列{c_n}是等比数列.

(2)解：∵c₁=a₁－1=－，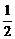

∴c_n=－，a_n=c_n+1=1－，a_n－1=1－.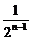

故当n≥2时，b_n=a_n－a_n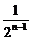－1=－=.又b₁=a₁=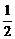，即b_n=(n∈N^*).

6.等比数列{a_n}的各项均为正数，其前n项中，数值最大的一项是54，若该数列的前n项之和为S_n，且S_n=80，S_2n=6560，求：

(1)前100项之和S₁₀₀.

(2)通项公式a_n.

解：设公比为q，∵S_2n－S_n=6480＞S_n，

∴q＞1.则最大项是a_n=a₁q^n－1(∵a_n＞0).　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ①

又S_n==80，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ②

S_2n==6560，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ③

由①②③解得a₁=2，q=3，则

(1)前100项之和S₁₀₀=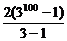=3¹⁰⁰－1.

(2)通项公式为a_n=2·3^n－1.

培养能力

5.定义一种运算“_*”对于任意非零自然数n满足以下运算性质：

(1)1_*1=1；

(2)(n+1)_*1=3(n_*1).

试求n_*1关于n的代数式.

解：“n_*1”是一个整体，联想数列通项形式，设n_*1=a_n，则a₁=1，a_n+1=3a_n，得a_n=3^n－1，即n_*1=3^n－1.

4.设{a_n}是首项为1的正项数列，且(n+1)a_n+1²－na_n²+a_n+1a_n=0(n∈N^*)，则它的通项公式a_n=___________________.

解析：分解因式可得［(n+1)a_n+1－na_n］·［a_n+1+a_n］=0，又a_n＞0，则(n+1)a_n+1－na_n=0，即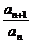=.又a₁=1，由累积法可得a_n=.

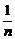答案：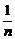

3.(2003年上海，8)若首项为a₁，公比为q的等比数列{a_n}的前n项和总小于这个数列的各项和，则首项a₁，公比q的一组取值可以是(a₁，q)=___________.

解析：由题意知＜且|q|＜1对n∈N都成立，∴a₁＞0，0＜q＜1.

答案：(1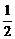，)(a₁＞0，0＜q＜1的一组数)

2.银行一年定期的年利率为r，三年定期的年利率为q，银行为吸收长期资金，鼓励储户存三年定期的存款，那么q的值应略大于

A.　　　　　　　　　　　　　　　　　　　　　　　 B.［(1+r)³－1］

C.(1+r)³－1　　　　　　　　　　　　　　　　　　　　　　　　 D.r

解析：由题意得(1+r)³＜1+3q，故q＞［(1+r)³－1］.

答案：B

1.若等比数列{a_n}的公比q＜0，前n项和为S_n，则S₈a₉与S₉a₈的大小关系是

A.S₈a₉＞S₉a₈ B.S₈a₉＜S₉a₈

C.S₈a₉=S₉a₈ D.不确定

解析：由等比数列通项公式和前n项和公式得

S₈·a₉－S₉·a₈

=－·a₁q³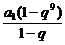－·a₁q⁷

===－a₁²q⁷.

又q＜0，则S₈·a₉－S₉·a₈＞0，即S₈·a₉＞S₉·a₈.

答案：A

2.若证{a_n}不是等比数列，只需证a_k²≠a_k－1a_k+1(k为常数，k∈N，且k≥2).

●闯关训练

夯实基础

1.{a_n}为等比数列是a_n+1²=a_n·a_n+2的充分但不必要条件.