
3.若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则 的取值范围是___________________.
的取值范围是___________________.
解析:在等差数列中,a1+a2=x+y;在等比数列中,xy=b1·b2.
∴ =
= =
= =
=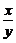 +
+ +2.
+2.
当x·y>0时,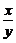 +
+ ≥2,故
≥2,故 ≥4;
≥4;
当x·y<0时,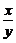 +
+ ≤-2,故
≤-2,故 ≤0.
≤0.
答案:[4,+∞)或(-∞,0]
2.公差不为零的等差数列{an}的第二、三及第六项构成等比数列,则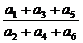 =_____.
=_____.
解析:设公差为d(d≠0),由题意a32=a2·a6,即(a1+2d)2=(a1+d)(a1+5d),解得d=-2a1,故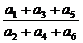 =
= =
=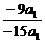 =
=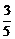 .
.
答案: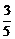
1.在等比数列{an}中,a5+a6=a(a≠0),a15+a16=b,则a25+a26的值是
A. B.
B. C.
C. D.
D.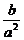
解析:由等比数列的性质得三个和成等比数列,由等比中项公式可得选项为C.
答案:C
5.(2002年北京,14)等差数列{an}中,a1=2,公差不为零,且a1,a3,a11恰好是某等比数列的前三项,那么该等比数列公比的值等于___________________.
解析:设a1,a3,a11成等比,公比为q,a3=a1·q=2q,a11=a1·q2=2q2.又{an}是等差数列,∴a11=a1+5(a3-a1),∴q=4.
答案:4
●典例剖析
[例1] (2005年春季北京,17)已知{an}是等比数列,a1=2,a3=18;{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{bn}的通项公式;
(2)求数列{bn}的前n项和Sn的公式;
(3)设Pn=b1+b4+b7+…+b3n-2,
Qn=b10+b12+b14+…+b2n+8,
其中n=1,2,…,试比较Pn与Qn的大小,并证明你的结论.
剖析:将已知转化成基本量,求出首项和公比后,再进行其他运算.
解:(1)设{an}的公比为q,由a3=a1q2得q2= =9,q=±3.
=9,q=±3.
当q=-3时,a1+a2+a3=2-6+18=14<20,
这与a1+a2+a3>20矛盾,故舍去.
当q=3时,a1+a2+a3=2+6+18=26>20,故符合题意.
设数列{bn}的公差为d,由b1+b2+b3+b4=26得4b1+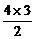 d=26.
d=26.
又b1=2,解得d=3,所以bn=3n-1.
(2)Sn=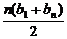 =
= n2+
n2+ n.
n.
(3)b1,b4,b7,…,b3n-2组成以3d为公差的等差数列,
所以Pn=nb1+ ·3d=
·3d=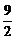 n2-
n2- n;
n;
b10,b12,b14,…,b2n+8组成以2d为公差的等差数列,b10=29,
所以Qn=nb10+ ·2d=3n2+26n.
·2d=3n2+26n.
Pn-Qn=(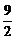 n2-
n2- n)-(3n2+26n)=
n)-(3n2+26n)= n(n-19).
n(n-19).
所以,对于正整数n,当n≥20时,Pn>Qn;
当n=19时,Pn=Qn;
当n≤18时,Pn<Qn.
评述:本题主要考查等差数列、等比数列等基本知识,考查逻辑思维能力、分析问题和解决问题的能力.
[例2] (2005年北京东城区模拟题)已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意正整数n均有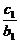 +
+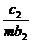 +
+ +…+
+…+ =(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
=(n+1)an+1成立,其中m为不等于零的常数,求数列{cn}的前n项和Sn.
剖析:(1)依已知可先求首项和公差,进而求出通项an和bn;(2)由题先求出{an}的通项公式后再求Sn.
解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2,整理得2a1d=d2.
∵a1=1,解得d=2(d=0不合题意舍去),
∴an=2n-1(n=1,2,3,…).
由b2=a2=3,b3=a5=9,易求得bn=3n-1(n=1,2,3,…).
(2)当n=1时,c1=6;
当n≥2时, =(n+1)an+1-nan=4n+1,
=(n+1)an+1-nan=4n+1,
∴cn=(4n+1)mn-1bn=(4n+1)(3m)n-1.
∴cn=
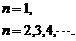
当3m=1,即m=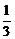 时,
时,
Sn=6+9+13+…+(4n+1)
=6+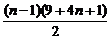
=6+(n-1)(2n+5)=2n2+3n+1.
当3m≠1,即m≠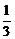 时,
时,
Sn=c1+c2+…+cn,即
Sn=6+9·(3m)+13·(3m)2+…+(4n-3)(3m)n-2+(4n+1)(3m)n-1. ①
3mSn=6·3m+9·(3m)2+13·(3m)3+…+(4n-3)(3m)n-1+(4n+1)(3m)n. ②
①-②得
(1-3m)Sn=6+3·3m+4·(3m)2+4·(3m)3+…+4·(3m)n-1-(4n+1)(3m)n
=6+9m+4[(3m)2+(3m)3+…+(3m)n-1]-(4n+1)(3m)n
=6+9m+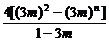 -(4n+1)(3m)n.
-(4n+1)(3m)n.
∴Sn= +
+ .
.
∴Sn=
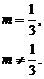
评述:本题主要考查了数列的基本知识和解决数列问题的基本方法.如“基本量法”“错位相减求和法”等.
[例3] (2005年北京海淀区模拟题)在等比数列{an}(n∈N*)中,a1>1,公比q>0.设bn=log2an,且b1+b3+b5=6,b1b3b5=0.
(1)求证:数列{bn}是等差数列;
(2)求{bn}的前n项和Sn及{an}的通项an;
(3)试比较an与Sn的大小.
剖析:(1)定义法即可解决.(2)先求首项和公差及公比.(3)分情况讨论.
(1)证明:∵bn=log2an,∴bn+1-bn=log2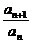 =log2q为常数.∴数列{bn}为等差数列且公差d=log2q.
=log2q为常数.∴数列{bn}为等差数列且公差d=log2q.
(2)解:∵b1+b3+b5=6,∴b3=2.
∵a1>1,∴b1=log2a1>0.
∵b1b3b5=0,∴b5=0.
∴ 解得
解得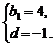
∴Sn=4n+ ×(-1)=
×(-1)=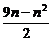 .
.
∵ ∴
∴
∴an=25-n(n∈N*).
(3)解:显然an=25-n>0,当n≥9时,Sn= ≤0.
≤0.
∴n≥9时,an>Sn.
∵a1=16,a2=8,a3=4,a4=2,a5=1,a6= ,a7=
,a7= ,a8=
,a8=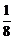 ,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4,
,S1=4,S2=7,S3=9,S4=10,S5=10,S6=9,S7=7,S8=4,
∴当n=3,4,5,6,7,8时,an<Sn;
当n=1,2或n≥9时,an>Sn.
评述:本题主要考查了数列的基本知识和分类讨论的思想.
●闯关训练
夯实基础
4.(2004年春季上海,12)在等差数列{an}中,当ar=as(r≠s)时,数列{an}必定是常数列,然而在等比数列{an}中,对某些正整数r、s(r≠s),当ar=as时,非常数列{an}的一个例子是___________________.
解析:只需选取首项不为0,公比为-1的等比数列即可.
答案:a,-a,a,-a…(a≠0)
3.若关于x的方程x2-x+a=0和x2-x+b=0(a≠b)的四个根可组成首项为 的等差数列,则a+b的值是
的等差数列,则a+b的值是
A. B.
B.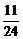 C.
C. D.
D.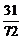
解析:依题意设四根分别为a1、a2、a3、a4,公差为d,其中a1= ,即a1+a2+a3+a4=1+1=2.又a1+a4=a2+a3,
,即a1+a2+a3+a4=1+1=2.又a1+a4=a2+a3,
所以a1+a4=a2+a3=1.
由此求得a4=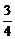 ,d=
,d= ,
,
于是a2= ,a3=
,a3= .
.
故a+b=a1a4+a2a3= ×
×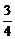 +
+ ×
× =
= =
=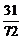 .
.
答案:D
2.已知数列{an}满足an+2=-an(n∈N*),且a1=1,a2=2,则该数列前2002项的和为
A.0 B.-3 C.3 D.1
解析:由题意,我们发现:a1=1,a2=2,a3=-a1=-1,a4=-a2=-2,a5=-a3=1,a6=
-a4=2,…,a2001=-a1999=1,a2002=-a2000=2,a1+a2+a3+a4=0.
∴a1+a2+a3+…+a2002=a2001+a2002=a1+a2=1+2=3.
答案:C
1.等比数列{an}的公比为q,则“q>1”是“对于任意自然数n,都有an+1>an”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
解析:当a1<0时,条件与结论均不能由一方推出另一方.
答案:D
2.对于等比数列:an=a1qn-1.可用指数函数的性质来理解.
当a1>0,q>1或a1<0,0<q<1时,等比数列是递增数列;
当a1>0,0<q<1或a1<0,q>1时,等比数列{an}是递减数列.
当q=1时,是一个常数列.
当q<0时,无法判断数列的单调性,它是一个摆动数列.
●点击双基
1.对于等差数列,∵an=a1+(n-1)d=dn+(a1-d),当d≠0时,an是n的一次函数,对应的点(n,an)是位于直线上的若干个点.当d>0时,函数是增函数,对应的数列是递增数列;同理,d=0时,函数是常数函数,对应的数列是常数列;d<0时,函数是减函数,对应的数列是递减函数.
若等差数列的前n项和为Sn,则Sn=pn2+qn(p、q∈R).当p=0时,{an}为常数列;当p≠0时,可用二次函数的方法解决等差数列问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com