3.(2004年北京西城区一模题)设0＜|α|＜，则下列不等式中一定成立的是

A.sin2α＞sinα　　　　　　　　　　　　　　　　　　　　　　　 B.cos2α＜cosα

C.tan2α＞tanα　　　　　　　　　　　　　　　　　　　　　　　 D.cot2α＜cotα

解析：由0＜|α|＜，知0＜2|α|＜且2|α|＞|α|，

∴cos2|α|＜cos|α|.∴cos2α＜cosα.

答案：B

2.(2001年春季北京)若A、B是锐角△ABC的两个内角，则点P(cosB－sinA，sinB－cosA)在

A.第一象限　　　　　　　　　　　　　　　　　　　　　　　　　　 B.第二象限

C.第三象限　　　　　　　　　　　　　　　　　　　　　　　　　　 D.第四象限

解析：∵△ABC为锐角三角形，

∴A+B＞.∴A＞－B，B＞－A.

∴sinA＞cosB，sinB＞cosA.

∴P在第二象限.

答案：B

1.已知sinx+cosx=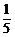，0≤x≤π，则tanx等于

A.－或－　　　　　　　　　　　　　　　　　　　　　　　　 B.－

C.－　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.或

解析：原式两边平方得2sinxcosx=－

－2sinxcosx=1－2sinxcosx=

sinx－cosx=，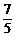

可得sinx=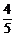，cosx=－.

∴tanx=－.

答案：B

3.三角函数与其他数学知识的联系.

特别要注意三角与几何、三角与平面向量的联系.

●点击双基

2.三角函数的恒等变形.

三角函数的化简、求值、证明多为综合题，突出对数学思想方法的考查.

1.三角函数的性质和图象变换.

4.10　 三角函数的应用

●知识梳理

2.利用同角三角函数的关系及诱导公式进行化简、求值、证明时，要细心观察题目的特征，注意培养学生观察、分析问题的能力，并注意做题后的总结，引导学生总结一般规律.如：“切割化弦”“1的巧代”，sinα+cosα、sinαcosα、sinα－cosα这三个式子间的关系.

拓展题例

[例1] 求sin²1°+sin²2°+…+sin²90°.

分析：sin²1°+cos²1°=sin²1°+sin²89°=1.

故可倒序相加求和.

解：设S=sin²0°+sin²1°+sin²2°+…+sin²90°，S=sin²90°+sin²89°+sin²88°+…+sin²0°，∴2S=(sin²0°+sin²90°)+…+(sin²90°+sin²0°)=1×91.∴S=45.5.

[例2] 已知sinα+cosβ=1，求y=sin²α+cosβ的取值范围.

分析：本题易错解为y=sin²α+1－sinα，sinα∈［－1，1］，然后求y的取值范围.

解：y=sin²α－sinα+1=(sinα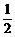－)²+.

∵sinα+cosβ=1，∴cosβ=1－sinα.

∴

∴sinα∈［0，1］.

∴y∈［，1］.

1.本课时概念多且杂，要求学生在预习的基础上，先准确叙述回忆，复习中注意“三基”的落实.

5.应用诱导公式，重点是“函数名称”与“正负号”的正确判断，一般常用“奇变偶不变，符号看象限”的口诀.

●教师下载中心

教学点睛