1.五点法作y=Asin(ωx+)的简图：五点取法是设x=ωx+，由x取0、、π、、2π来求相应的x值及对应的y值，再描点作图.

4.5　 三角函数的图象与性质(一)

●知识梳理

3.注意方程思想的应用.

拓展题例

[例1] 试证：=.

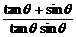证明：左边=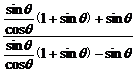

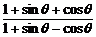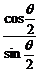====cot，

右边==

==cot，∴原等式成立.

[例2] 已知α、β∈(0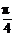，)，3sinβ=sin(2α+β)，4tan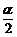=1－tan²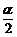.求α+β的值.

解：∵4tan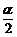=1－tan²，

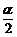∴2·tanα=1，tanα=.

∵3sinβ=sin(2α+β)，

∴3sinβ=sin(α+β)cosα+cos(α+β)sinα.

∴3sin(α+β)cosα－3cos(α+β)sinα

=sin(α+β)cosα+cos(α+β)sinα.

∴sin(α+β)cosα=2cos(α+β)sinα.

∴tan(α+β)=2tanα=1.∴α+β=.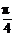

评述：角的变换是常用技巧.如2α+β=(α+β)+α，β=(α+β)－α等.

2.有条件的三角函数求值有两个关键：①三角函数各关系式及常用公式的熟练应用.②条件的合理应用：注意条件的整体功能，注意将条件适当简化、整理或重新改造组合，使其与所计算的式子更加吻合.

1.三角恒等式的证明实际上就是三角函数式的化简过程.

3.三角函数的应用主要是借用三角函数的值域求最值，这首先应将原函数通过降幂、辅助角公式等化成y=Asin(ωx+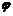)(A≠0，ω＞0)的形式，或者通过换元转化成二次函数，然后再求之.

●教师下载中心

教学点睛

2.条件等式的证明，通过认真观察，发现已知条件和待证等式之间的关系，选择适当的途径把条件用上去.常用方法有代入法、消去法、综合法(即从已知条件出发，以待证式为目标进行代数或三角恒等变形，逐步推出待证式)、分析法等.

1.证明三角恒等式的基本思路，是根据等式两端的特征，通过三角恒等变换，应用化繁为简、左右归一、变更命题等方法，使等式两端的“异”化为“同”.

9.锐角x、y满足sinycscx=cos(x+y)且x+y≠，求tany的最大值.

解：∵sinycscx=cos(x+y)，

∴sinycscx=cosxcosy－sinxsiny，

siny(sinx+cscx)=cosxcosy.

∴tany====≤=，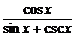

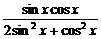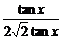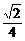当且仅当tanx=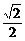时取等号.

∴tany的最大值为.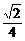

●思悟小结

8.(2005年春季北京，15)在△ABC中，sinA+cosA=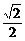，AC=2，AB=3，求tanA的值和△ABC的面积.

分析：本题主要考查三角恒等变形、三角形面积公式等基本知识，考查运算能力.

解法一：∵sinA+cosA=cos(A－45°)=，

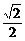∴cos(A－45°)=.

又0°＜A＜180°，

∴A－45°=60°，A=105°.

∴tanA=tan(45°+60°)==－2－.

∴sinA=sin105°=sin(45°+60°)

=sin45°cos60°+cos45°sin60°=.

∴S_△ABC=AC·ABsinA

=·2·3·

=(+).

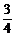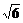解法二：∵sinA+cosA=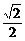，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

∴(sinA+cosA)²=.∴2sinAcosA=－.

∵0°＜A＜180°，∴sinA＞0，cosA＜0.

∴90°＜A＜180°.

∵(sinA－cosA)²=1－2sinAcosA=，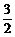

∴sinA－cosA=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

①+②得sinA=.

①－②得cosA=.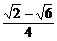

∴tanA==·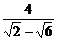=－2－.

(以下同解法一)

探究创新