2.当函数的定义域为关于原点对称的区间时，判断函数的奇偶性一般运用奇偶性的定义，有时亦可应用与定义等价的命题，如f(－x)∶f(x)=1(f(x)≠0)，则f(x)为偶函数，若f(－x)∶f(x)=－1　(f(x)≠0)，则f(x)为奇函数，或由f(－x)±f(x)=0来判断奇偶性.

1.函数的单调性是在定义域或定义域的某个子区间上考虑的，要比较两三角函数值的大小一般先将它们化归为同一单调区间的同名函数再由该函数的单调性来比较大小.

9.已知P(1，cosx)，Q(cosx，1)，x∈［－，］.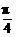

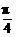(1)求向量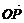和的夹角θ的余弦用x表示的函数f(x)；

(2)求θ的最值.

解：(1)∵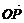·=2cosx，

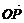||·||=1+cos²x，

∴f(x)=cosθ=.

(2)cosθ==，

x∈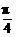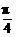［－，］，cosx∈［，1］.

∴2≤cosx+≤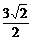，≤f(x)≤1，即≤cosθ≤1.

∴θ_max=arccos，θ_min=0.

●思悟小结

8.若｜log_cosαsinα｜＞｜log_sinαcosα｜(α为锐角)，求α的取值范围.

解：∵α为锐角，0＜cosα＜1，0＜sinα＜1，

∴log_cosαsinα＞0，log_sinαcosα＞0.

∴原式就是log_cosαsinα＞log_sinαcosα

＞1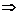(log_cosαsinα)²＞1

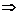log_cosαsinα＞1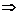sinα＜cos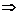α0＜α＜.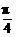

探究创新

7.设x∈［0，］，f(x)=sin(cosx)，g(x)=cos(sinx)，求f(x)、g(x)的最大值.

解：∵在x∈［0，］上，y=cosx是单调递减的，且cosx∈［0，1］，而y=sinx是单调递增的，且sinx∈［0，1］，

∴f(x)=sin(cosx)∈［0，sin1］，

g(x)=cos(sinx)∈［cos1，1］.

∴f(x)的最大值是sin1，g(x)的最大值是1.

6.当α∈(0，π)时，求y=－.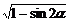

解：y=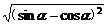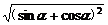－=｜sinα－cosα｜－｜sinα+cosα｜.

(1)当α∈(0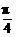，］时，有sinα＜cosα，sinα+cosα＞0，

∴y=cosα－sinα－sinα－cosα=－2sinα.

(2)当α∈(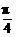，)时，sinα＞cosα，sinα+cosα≥0，

∴y=sinα－cosα－sinα－cosα=－2cosα.

(3)当α∈(，π)时，有sinα＞cosα，sinα+cosα＜0，∴y=sinα－cosα+sinα+cosα=2sinα.

培养能力

5.给出下列命题：

①正切函数的图象的对称中心是唯一的；

②y=|sinx|、y=|tanx|的周期分别为π、；

③若x₁＞x₂，则sinx₁＞sinx₂；

④若f(x)是R上的奇函数，它的最小正周期为T，则f(－)=0.

其中正确命题的序号是____________.

答案：④

4.若f(x)具有性质：

①f(x)为偶函数，②对任意x∈R，都有f(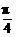－x)=f(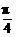+x)，则f(x)的解析式可以是_______.(只写一个即可)

答案：f(x)=a或f(x)=cos4x或f(x)=|sin2x|等.

3.(2004年福建，11)定义在R上的函数f(x)满足f(x)=f(x+2)，当x∈［3，5］时，f(x)=2－|x－4|，则

A.f(sin)＜f(cos)

B.f(sin1)＞f(cos1)

C.f(cos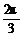)＜f(sin)

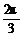D.f(cos2)＞f(sin2)

解析：由f(x)=f(x+2)知T=2，

又∵x∈［3，5］时，f(x)=2－|x－4|，

可知当3≤x≤4时，f(x)=－2+x.

当4＜x≤5时，f(x)=6－x.其图如下，故在(－1，0)上是增函数，在(0，1)上是减函数.

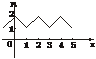
又由|cos2|＜|sin2|，

∴f(cos2)＞f(sin2).

答案：D

2.为了使y=sinωx(ω＞0)在区间［0，1］上至少出现50次最大值，则ω的最小值是

A.98π　　　　　　　　　　　　 B.　　　　　　　　　　　 C.　　　　　　　　　　　 D.100π

解析：49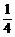×T≤1，即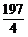×≤1，

∴ω≥.

答案：B

思考：若条件改为在［x₀，x₀+1］上至少出现50次最大值呢？