1.理解向量的概念，掌握向量的几何表示，了解共线向量的概念.

∴cos²α+cos²β+cos²γ=2≥3.

∴cos²αcos²βcos²γ≤()³.

∴cosαcosβcosγ≤==.

答案：

2.例题也可由学生独立完成，并从中总结方法.

拓展题例

[例题] (2001年春季全国)已知sin²α+sin²β+sin²γ=1(α、β、γ均为锐角)，那么cosαcosβcosγ的最大值等于_______.

解析：∵sin²α+sin²β+sin²γ=1，

1.建议让学生从做“点击双基”中体会总结方法.

3.注意题中的隐含条件.

●教师下载中心

教学点睛

2.三角函数的最值都是在给定区间上取得的，因而特别要注意题设中所给出的区间.

(1)求三角函数最值时，一般要进行一些代数变换和三角变换，要注意函数有意义的条件及弦函数的有界性.

(2)含参数函数的最值问题，要注意参数的作用和影响.

1.求三角函数最值的常用方法有：①配方法(主要利用二次函数理论及三角函数的有界性)；②化为一个角的三角函数(主要利用和差角公式及三角函数的有界性)；③数形结合法(常用到直线的斜率关系)；④换元法(如万能公式，将三角问题转化为代数问题)；⑤基本不等式法等.

9.设函数f(x)=asinωx+bcosωx(ω＞0)的最小正周期为π，并且当x=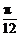时，有最大值f(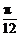)=4.

(1)求a、b、ω的值；

(2)若角α、β的终边不共线，f(α)=f(β)=0，求tan(α+β)的值.

解：(1)由=π，ω＞0得ω=2.

∴f(x)=asin2x+bcos2x.

由x=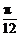时，f(x)的最大值为4，

得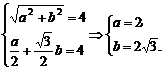

(2)由(1)得f(x)=4sin(2x+).

依题意有4sin(2α+)=4sin(2β+)=0.

∴sin(2α+)－sin(2β+)=0.

∴cos(α+β+)sin(α－β)=0(和差化积公式见课本).

∵α、β的终边不共线，即α－β≠kπ(k∈Z)，

故sin(α－β)≠0.

∴α+β=kπ+(k∈Z).∴tan(α+β)=.

●思悟小结

8.(2005年北京海淀区高三期末练习)已知向量a=(cos，sin)，b=(cos，－sin)，c=(，－1)，其中x∈R.

(1)当a⊥b时，求x值的集合；

(2)求|a－c|的最大值.

解：(1)由a⊥b得a·b=0，即coscos－sinsin =0.

则cos2x=0，得x=+(k∈Z).

∴{x|x=+，k∈Z}为所求.

(2)|a－c|²=(cos－)²+(sin+1)²=5+4sin(－)，

∴|a－c|有最大值3.

探究创新

7.已知对任意x，恒有y≥sin²x+4sin²xcos²x，求y的最小值.

解：令u=sin²x+4sin²xcos²x，

则u=sin²x+sin²2x=(1－cos2x)+(1－cos²2x)=－cos²2x－cos2x+=－(cos2x+)²+，

得u_max=.由y≥u知y_min=.