
6.设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
解:e12=4,e22=1,e1·e2=2×1×cos60°=1,
∴(2te1+7e2)·(e1+te2)=2te12+(2t2+7)e1·e2+7te22=2t2+15t+7.∴2t2+15t+7<0.
∴-7<t<- .设2te1+7e2=λ(e1+te2)(λ<0)
.设2te1+7e2=λ(e1+te2)(λ<0)

 2t2=7
2t2=7 t=-
t=-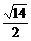 ,
,
∴λ=- .
.
∴当t=-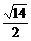 时,2te1+7e2与e1+te2的夹角为π.
时,2te1+7e2与e1+te2的夹角为π.
∴t的取值范围是(-7,-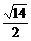 )∪(-
)∪(-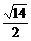 ,-
,- ).
).
思考讨论
向量a、b的夹角为钝角,则cos〈a,b〉<0,它们互为充要条件吗?
培养能力
5.l1、l2是不共线向量,且a=-l1+3l2,b=4l1+2l2,c=-3l1+12l2,若b、c为一组基底,求向量a.
解:设a=λ1b+λ2c,即-l1+3l2=λ1(4l1+2l2)+λ2(-3l1+12l2),
即-l1+3l2=(4λ1-3λ2)l1+(2λ1+12λ2)l2,
∴
解得λ1=-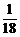 ,λ2=
,λ2= ,故a=-
,故a=-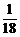 b+
b+ c.
c.
4.设四边形ABCD中,有 =
=
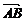 且|
且| |=|
|=|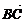 |,则这个四边形是
|,则这个四边形是
A.平行四边形 B.矩形
C.等腰梯形 D.菱形
解析:∵ =
=
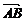 ,∴DC∥AB,且DC≠AB.又|
,∴DC∥AB,且DC≠AB.又| |=|
|=|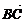 |,∴四边形为等腰梯形.
|,∴四边形为等腰梯形.
答案:C
3.在四边形ABCD中,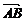 -
- -
- 等于
等于
A. B.
B. C.
C. D.
D.
解析: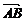 -
- -
- =
=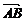 -
- =
=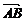 +
+ =
= .
.
答案:C
2.若a、b为非零向量,且|a+b|=|a|+|b|,则有
A.a∥b且a、b方向相同 B.a=b
C.a=-b D.以上都不对
解析:a、b为非零向量,且|a+b|=|a|+|b|,∴a∥b且方向相同.
答案:A
1.(2004年广东,1)已知平面向量a=(3,1),b=(x,-3)且a⊥b,则x等于
A.3 B.1 C.-1 D.-3
解析:由a⊥b,则3x-3=0,∴x=1.
答案:B
5.若a=“向东走8 km”,b=“向北走8 km”,则|a+b|=_______,a+b的方向是_______.
解析:|a+b|= =8
=8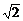 (km).
(km).
答案:8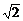 km 东北方向
km 东北方向
●典例剖析
[例1] 已知向量a、b满足|a|=1,|b|=2,|a-b|=2,则|a+b|等于
A.1 B.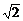 C.
C. D.
D.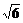
剖析:欲求|a+b|,一是设出a、b的坐标求,二是直接根据向量模计算.
解法一:设a=(x1,y1),b=(x2,y2),则x12+y12=1,x22+y22=4,a-b=(x1-x2,y1-y2),
∴(x1-x2)2+(y1-y2)2=4.
∴x12-2x1x2+x22+y12-2y1y2+y22=4.
∴1-2x1x2-2y1y2=0.∴2x1x2+2y1y2=1.
∴(x1+x2)2+(y1+y2)2=1+4+2x1x2+2y1y2=5+1=6.
∴|a+b|=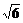 .
.
解法二:∵|a+b|2+|a-b|2=2(|a|2+|b|2),
∴|a+b|2=2(|a|2+|b|2)-|a-b|2
=2(1+4)-22=6.
∴|a+b|=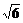 .故选D.
.故选D.
深化拓展
此题也可以利用“解斜三角形”的方法进行处理.
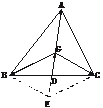
[例2] 如图,G是△ABC的重心,求证: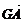 +
+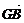 +
+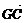 =0.
=0.
剖析:要证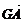 +
+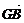 +
+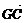 =0,只需证
=0,只需证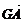 +
+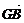 =-
=-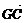 ,即只需证
,即只需证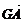 +
+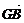 与
与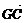 互为相反的向量.
互为相反的向量.
证明:以向量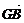 、
、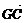 为邻边作平行四边形GBEC,则
为邻边作平行四边形GBEC,则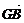 +
+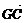 =
=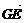 =2
=2 .又由G为△ABC的重心知
.又由G为△ABC的重心知
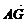 =2
=2 ,从而
,从而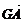 =-2
=-2 .
.
∴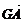 +
+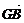 +
+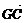 =-2
=-2 +2
+2 =0.
=0.
评述:向量的加法可以用几何法进行.正确理解向量的各种运算的几何意义,能进一步加深对“向量”的认识,并能体会用向量处理问题的优越性.
深化拓展
此题也可用向量的坐标运算进行证明.
[例3] 设 、
、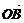 不共线,点P在AB上,求证:
不共线,点P在AB上,求证: =λ
=λ +μ
+μ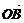 且λ+μ=1,λ、μ∈R.
且λ+μ=1,λ、μ∈R.
剖析:∵点P在AB上,可知 与
与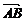 共线,得
共线,得 =t
=t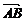 .再用以O为起点的向量表示.
.再用以O为起点的向量表示.
证明:∵P在AB上,∴ 与
与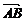 共线.
共线.
∴ =t
=t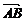 .∴
.∴ -
- =t(
=t(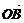 -
- ).
).
∴ =
= +t
+t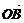 -t
-t =(1-t)
=(1-t) +t
+t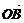 .
.
设1-t=λ,t=μ,则 =λ
=λ +μ
+μ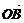 且λ+μ=1,λ、μ∈R.
且λ+μ=1,λ、μ∈R.
评述:本例的重点是考查平面向量的基本定理,及对共线向量的理解及应用.
深化拓展
①本题也可变为 ,
,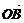 不共线,若
不共线,若 =λ
=λ +μ
+μ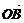 ,且λ+μ=1,λ∈R,μ∈R,求证:A、B、P三点共线.
,且λ+μ=1,λ∈R,μ∈R,求证:A、B、P三点共线.
提示:证明 与
与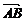 共线.
共线.
②当λ=μ= 时,
时, =
= (
( +
+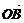 ),此时P为AB的中点,这是向量的中点公式.
),此时P为AB的中点,这是向量的中点公式.
[例4] 若a、b是两个不共线的非零向量(t∈R).
(1)若a与b起点相同,t为何值时,a、tb、 (a+b)三向量的终点在一直线上?
(a+b)三向量的终点在一直线上?
(2)若|a|=|b|且a与b夹角为60°,那么t为何值时,|a-tb|的值最小?
解:(1)设a-tb=m[a- (a+b)](m∈R),
(a+b)](m∈R),
化简得(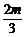 -1)a=(
-1)a=( -t)b.
-t)b.
∵a与b不共线,
∴
∴t= 时,a、tb、
时,a、tb、 (a+b)的终点在一直线上.
(a+b)的终点在一直线上.
(2)|a-tb|2=(a-tb)2=|a|2+t2|b|2-2t|a||b|cos60°=(1+t2-t)|a|2,∴t= 时,|a-tb|有最小值
时,|a-tb|有最小值 |a|.
|a|.
评述:用两个向量共线的充要条件,可解决平面几何中的平行问题或共线问题.
思考讨论
两个向量共线与两条线段在一条直线上是否一样?
●闯关训练
夯实基础
4.e1、e2是不共线的向量,a=e1+ke2,b=ke1+e2,则a与b共线的充要条件是实数k等于
A.0 B.-1 C.-2 D.±1
解析:a与b共线 存在实数m,使a=mb,
存在实数m,使a=mb,
即e1+ke2=mke1+me2.又e1、e2不共线,
∴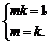 ∴k=±1.
∴k=±1.
答案:D
3.若ABCD为正方形,E是CD的中点,且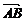 =a,
=a, =b,则
=b,则 等于
等于
A.b+ a B.b-
a B.b- a
a
C.a+ b D.a-
b D.a- b
b
解析: =
=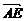 -
-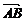 =
= +
+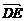 -
-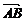 =
= +
+
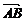 -
-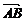 =b-
=b- a.
a.
答案:B
2.(2004年浙江,文4)已知向量a=(3,4),b=(sinα,cosα),且a∥b,则tanα等于
A.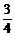 B.-
B.-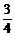 C.
C.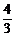 D.-
D.-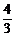
解析:由a∥b,∴3cosα=4sinα.∴tanα=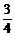 .
.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com