
3.已知a=(λ,2),b=(-3,5),且a与b的夹角为钝角,则λ的取值范围是
A.λ> B.λ≥
B.λ≥
C.λ< D.λ≤
D.λ≤
解析:∵a与b的夹角为钝角,∴cos〈a,b〉<0.
∴a·b<0.∴-3λ+10<0.∴λ> .
.
答案:A
2.若向量a与b的夹角为60°,|b|=4,(a+2b)·(a-3b)=-72,则向量a的模是
A.2 B.4 C.6 D.12
解析:(a+2b)·(a-3b)=|a|2-|a||b|cos60°-6|b|2=|a|2-2|a|-96=-72,∴|a|2-2|a|-24=0.∴(|a|-6)·(|a|+4)=0.∴|a|=6.
答案:C
1.(2004年全国Ⅰ,3)已知a、b均为单位向量,它们的夹角为60°,那么|a+3b|等于
A. B.
B.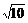 C.
C.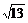 D.4
D.4
解析:|a+3b|= =
=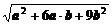 =
= =
=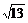 .
.
答案:C
4.向量数量积的坐标运算:
设a=(x1,y1),b=(x2,y2),则
(1)a·b=x1x2+y1y2;
(2)|a|= ;
;
(3)cos〈a,b〉= ;
;
(4)a⊥b a·b=0
a·b=0 x1x2+y1y2=0.
x1x2+y1y2=0.
思考讨论
(a·b)c与a(b·c)是否相等?
●点击双基
3.运算律:(1)a·b=b·a;(2)(λa)·b=λ(a·b)=a·(λb);(3)(a+b)·c=a·c+b·c.
2.数量积的性质:设e是单位向量,〈a,e〉=θ.
(1)e·a=a·e=|a|cosθ.
(2)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|,特别地,a·a=|a|2,或|a|= .
.
(3)a⊥b a·b=0.
a·b=0.
(4)cosθ=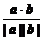 .
.
(5)|a·b|≤|a||b|.
1.数量积的概念:
(1)向量的夹角:如下图,已知两个非零向量a和b,作 =a,
=a, =b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角,记作〈a,b〉.
=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角,记作〈a,b〉.

(2)数量积的定义:已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b,即a·b=|a||b|cosθ.
(3)数量积的几何意义:数量积a·b等于a的模与b在a方向上的投影|b|cosθ的乘积.
5.2 向量的数量积
●知识梳理
4.强化数学思想的教学,尤其是数形结合思想、化归思想等.
拓展题例
[例题] 对任意非零向量a、b,求证:|a|-|b|≤|a±b|≤|a|+|b|.
证明:分三种情况考虑.
(1)当a、b共线且方向相同时,|a|-|b|<|a+b|=|a|+|b|,|a|-|b|=|a-b|<|a|+|b|.
(2)当a、b共线且方向相反时,∵a-b=a+(-b),a+b=a-(-b),利用(1)的结论有||a|-|b||<|a+b|<|a|+|b|,|a|-|b|<|a-b|=|a|+|b|.
(3)当a,b不共线时,设 =a,
=a,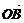 =b,作
=b,作 =
= +
+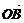 =a+b,
=a+b, =
= -
-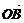 =a-b,利用三角形两边之和大于第三边,两边之差小于第三边,得||a|-|b||<|a±b|<|a|+|b|.
=a-b,利用三角形两边之和大于第三边,两边之差小于第三边,得||a|-|b||<|a±b|<|a|+|b|.
综上得证.
3.向量的加法、减法运算既要注重几何运算,又要注重代数运算.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com