
3.点的平移公式描述的是平移前、后点的坐标与平移向量坐标三者之间的关系,
特别提示
2.线段的定比分点是研究共线的三点P1,P,P2坐标间的关系.应注意:(1)点P是不同于P1,P2的直线P1P2上的点;(2)实数λ是P分有向线段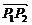 所成的比,即P1→P,P→P2的顺序,不能搞错;(3)定比分点的坐标公式
所成的比,即P1→P,P→P2的顺序,不能搞错;(3)定比分点的坐标公式 (λ≠-1).
(λ≠-1).
1.设A(x1,y1),B(x2,y2),
则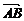 =(x2-x1,y2-y1).
=(x2-x1,y2-y1).
∴|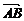 |=
|= .
.
5.3 两点间距离公式、线段的定比分点与图形的平移
●知识梳理
3.要让学生掌握向量的夹角的含义.要会用cosθ=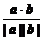 或cosθ=
或cosθ= 求两向量的夹角.
求两向量的夹角.
拓展题例
[例题] 在△ABC中,(1)若 =a,
=a, =b,求证:S△ABC=
=b,求证:S△ABC=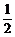
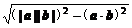 ;(2)若
;(2)若 =(a1,a2),
=(a1,a2), =(b1,b2),求证:△ABC的面积S△=
=(b1,b2),求证:△ABC的面积S△=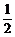 |a1b2-a2b1|.
|a1b2-a2b1|.
证明:(1)设a、b的夹角为θ,△ABC的面积S△=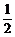 |
| ||
|| |sinθ=
|sinθ=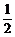 |a||b|sinθ.
|a||b|sinθ.
∵sin2θ=1-cos2θ=1-(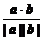 )2,
)2,
∴S△2= (|a||b|)2sin2θ
(|a||b|)2sin2θ
= (|a||b|)2[1-(
(|a||b|)2[1-(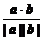 )2]
)2]
= [(|a||b|)2-(a·b)2].
[(|a||b|)2-(a·b)2].
∴S△=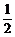
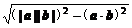 .
.
(2)记 =a,
=a, =b,则a=(a1,a2),b=(b1,b2).∴|a|2=a12+a22,|b|2=b12+b22,
=b,则a=(a1,a2),b=(b1,b2).∴|a|2=a12+a22,|b|2=b12+b22,
|a·b|2=(a1b1+a2b2)2.
由(1)可知S△=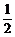
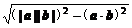
=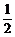
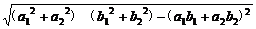
=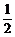
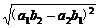 ,
,
∴S△=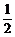 |a1b2-a2b1|.
|a1b2-a2b1|.
评述:(1)是用数量积给出的三角形的面积公式;(2)是用向量坐标给出的三角形的面积公式.
2.向量的数量积是向量之间的一种乘法运算,它是向量与向量的运算,结果却是一个数量.
3.向量a与b的夹角:(1)当a与b平移成有公共起点时两向量所成的角才是夹角;(2)0°≤〈a,b〉≤180°;(3)cos〈a,b〉=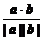 =
= .
.
●教师下载中心
教学点睛
2.向量的数量积是向量之间的一种乘法运算,它是向量与向量的运算,结果却是一个数量,所以向量的数量积的坐标表示是纯数量的坐标表示.
1.平面向量的数量积及其几何意义是本节的重点,用数量积处理向量垂直问题,向量的长度、角度问题是难点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com