
3.(2004年全国Ⅳ,理11)△ABC中,a、b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=30°,△ABC的面积为 ,那么b等于
,那么b等于
A. B.1+
B.1+
C. D.2+
D.2+
解析:∵a、b、c成等差数列,∴2b=a+c.平方得a2+c2=4b2-2ac.又△ABC的面积为 ,且∠B=30°,故由S△ABC=
,且∠B=30°,故由S△ABC= acsinB=
acsinB= acsin30°=
acsin30°=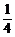 ac=
ac= ,得ac=6.∴a2+c2=4b2-12.由余弦定理,得cosB=
,得ac=6.∴a2+c2=4b2-12.由余弦定理,得cosB= =
=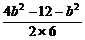 =
= =
= ,解得b2=4+2
,解得b2=4+2 .又b为边长,∴b=1+
.又b为边长,∴b=1+ .
.
答案:B
2.下列条件中,△ABC是锐角三角形的是
A.sinA+cosA= B.
B.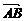 ·
·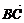 >0
>0
C.tanA+tanB+tanC>0 D.b=3,c=3 ,B=30°
,B=30°
解析:由sinA+cosA=
得2sinAcosA=-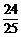 <0,∴A为钝角.
<0,∴A为钝角.
由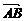 ·
·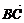 >0,得
>0,得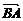 ·
·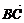 <0,∴cos〈
<0,∴cos〈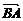 ,
,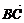 〉<0.∴B为钝角.
〉<0.∴B为钝角.
由tanA+tanB+tanC>0,得tan(A+B)·(1-tanAtanB)+tanC>0.
∴tanAtanBtanC>0,A、B、C都为锐角.
由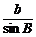 =
= ,得sinC=
,得sinC= ,∴C=
,∴C= 或
或 .
.
答案:C
1.(2002年上海)在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
解析:由2cosBsinA=sinC得 ×a=c,∴a=b.
×a=c,∴a=b.
答案:C
2.余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
a2=b2+c2-2bccosA; ①
b2=c2+a2-2cacosB; ②
c2=a2+b2-2abcosC. ③
在余弦定理中,令C=90°,这时cosC=0,所以c2=a2+b2.
由此可知余弦定理是勾股定理的推广.由①②③可得
cosA= ;
;
cosB= ;
;
cosC= .
.
利用余弦定理,可以解决以下两类有关三角形的问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.
特别提示
两定理的形式、内容、证法及变形应用必须引起足够的重视,通过向量的数量积把三角形和三角函数联系起来,用向量方法证明两定理,突出了向量的工具性,是向量知识应用的实例.另外,解三角形问题可能出现一解、两解或无解的情况,这时应结合“三角形中大边对大角定理及几何作图来帮助理解”.
●点击双基
1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即 =
=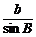 =
= .
.
利用正弦定理,可以解决以下两类有关三角形的问题.
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角.(从而进一步求出其他的边和角)
5.4 解斜三角形
●知识梳理
3.平移前后坐标之间的关系极易出错,要引导学生弄清知识的形成过程不要死记硬背.
拓展题例
[例1] (2004年豫南三市联考)已知f(A,B)=sin22A+cos22B-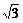 sin2A-cos2B+2.
sin2A-cos2B+2.
(1)设△ABC的三内角为A、B、C,求f(A,B)取得最小值时,C的值;
(2)当A+B=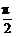 且A、B∈R时,y=f(A,B)的图象按向量p平移后得到函数y=2cos2A的图象,求满足上述条件的一个向量p.
且A、B∈R时,y=f(A,B)的图象按向量p平移后得到函数y=2cos2A的图象,求满足上述条件的一个向量p.
解:(1)f(A,B)=(sin2A-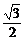 )2+(cos2B-
)2+(cos2B- )2+1,
)2+1,
由题意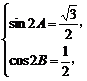 得
得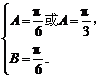
∴C=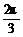 或C=
或C=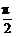 .
.
(2)∵A+B=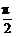 ,∴2B=π-2A,cos2B=-cos2A.
,∴2B=π-2A,cos2B=-cos2A.
∴f(A,B)=cos2A-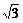 sin2A+3=2cos(2A+
sin2A+3=2cos(2A+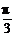 )+3=2cos2(A+
)+3=2cos2(A+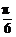 )+3.
)+3.
从而p=(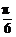 ,-3)(只要写出一个符合条件的向量p即可).
,-3)(只要写出一个符合条件的向量p即可).
[例2] 设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平移t、s单位长度后,得到曲线C1.
(1)写出曲线C1的方程;
(2)证明:曲线C与C1关于点A( ,
, )对称.
)对称.
(1)解:C1:y-s=(s-t)3-(x-t). ①
(2)分析:要证明曲线C1与C关于点A( ,
, )对称,只需证明曲线C1上任意一个点关于A点的对称点都在曲线C上,反过来,曲线C上任意一个点关于A点的对称点都在曲线C1上即可.
)对称,只需证明曲线C1上任意一个点关于A点的对称点都在曲线C上,反过来,曲线C上任意一个点关于A点的对称点都在曲线C1上即可.
证明:设P1(x1,y1)为曲线C1上任意一点,它关于点A( ,
, )的对称点为
)的对称点为
P(t-x1,s-y1),把P点坐标代入曲线C的方程,左=s-y1,右=(t-x1)3-(t-x1).
由于P1在曲线C1上,∴y1-s=(x1-t)3-(x1-t).
∴s-y1=(t-x1)3-(t-x1),即点P(t-x1,s-y1)在曲线C上.
同理可证曲线C上任意一点关于点A的对称点都在曲线C1上.
从而证得曲线C与C1关于点A( ,
, )对称.
)对称.
2.定比分点坐标公式要用活不要死记.可设出坐标利用向量相等列方程组.该解法充分体现了向量(形)与数之间的转化具有一般性.
1.线段的定比分点公式 =λ
=λ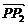 ,该式中已知P1、P2及λ可求分点P的坐标,并且还要注意公式的变式在P1、P2、P、λ中知三可求第四个量.
,该式中已知P1、P2及λ可求分点P的坐标,并且还要注意公式的变式在P1、P2、P、λ中知三可求第四个量.
4.配凑法、待定系数法、对应点代入法是确定平移向量的重要方法.
●教师下载中心
教学点睛
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com