
8.在△ABC中,BC=a,顶点A在平行于BC且与BC相距为a的直线上滑动,求 的取值范围.
的取值范围.
解:令AB=kx,AC=x(k>0,x>0),则总有sinB= ,sinC=
,sinC= (图略),且由正弦定理得sinB=
(图略),且由正弦定理得sinB=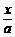 sinA,所以a2=kx2·sinBsinC=kx2sinA,由余弦定理,可得cosA=
sinA,所以a2=kx2·sinBsinC=kx2sinA,由余弦定理,可得cosA= =
= (k+
(k+ -sinA),所以k+
-sinA),所以k+ =sinA+2cosA≤
=sinA+2cosA≤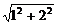 =
= .所以k2-
.所以k2- k+1≤0,所以
k+1≤0,所以 ≤k≤
≤k≤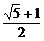 .
.
所以 的取值范围为[
的取值范围为[ ,
,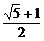 ].
].
探究创新
7.已知△ABC中,2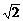 (sin2A-sin2C)=(a-b)sinB,外接圆半径为
(sin2A-sin2C)=(a-b)sinB,外接圆半径为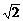 .
.
(1)求∠C;
(2)求△ABC面积的最大值.
解:(1)由2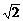 (sin2A-sin2C)=(a-b)·sinB得2
(sin2A-sin2C)=(a-b)·sinB得2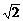 (
(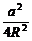 -
- )=(a-b)
)=(a-b) .
.
又∵R=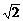 ,
,
∴a2-c2=ab-b2.∴a2+b2-c2=ab.
∴cosC= =
= .
.
又∵0°<C<180°,∴C=60°.
(2)S= absinC=
absinC= ×
× ab
ab
=2 sinAsinB=2
sinAsinB=2 sinAsin(120°-A)
sinAsin(120°-A)
=2 sinA(sin120°cosA-cos120°sinA)
sinA(sin120°cosA-cos120°sinA)
=3sinAcosA+ sin2A
sin2A
= sin2A-
sin2A- sin2Acos2A+
sin2Acos2A+
= sin(2A-30°)+
sin(2A-30°)+ .
.
∴当2A=120°,即A=60°时,Smax= .
.
6.在△ABC中,角A、B、C所对的边分别为a、b、c,依次成等比数列,求y= 的取值范围.
的取值范围.
解:∵b2=ac,∴cosB= =
= =
= (
( +
+ )-
)- ≥
≥ .
.
∴0<B≤ ,
,
y= =
= =sinB+cosB=
=sinB+cosB=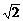 sin(B+
sin(B+ ).∵
).∵ <B+
<B+ ≤
≤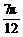 ,
,
∴ <sin(B+
<sin(B+ )≤1.故1<y≤
)≤1.故1<y≤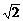 .
.
5.在△ABC中,由已知条件解三角形,其中有两解的是
A.b=20,A=45°,C=80° B.a=30,c=28,B=60°
C.a=14,b=16,A=45° D.a=12,c=15,A=120°
解析:由a=14,b=16,A=45°及正弦定理,得 =
=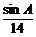 ,所以sinB=
,所以sinB= .因而B有两值.
.因而B有两值.
答案:C
培养能力
4.在△ABC中,若∠C=60°,则 =_______.
=_______.
解析: =
=
= . (*)
. (*)
∵∠C=60°,∴a2+b2-c2=2abcosC=ab.
∴a2+b2=ab+c2.
代入(*)式得 =1.
=1.
答案:1
3.在△ABC中,角A、B、C所对的边分别是a、b、c,若三角形的面积S=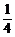 (a2+b2-c2),则∠C的度数是_______.
(a2+b2-c2),则∠C的度数是_______.
解析:由S=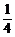 (a2+b2-c2)得
(a2+b2-c2)得 absinC=
absinC=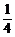 ·2abcosC.∴tanC=1.∴C=
·2abcosC.∴tanC=1.∴C= .
.
答案:45°
2.如图,△ABC是简易遮阳棚,A、B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为了使遮阴影面ABD面积最大,遮阳棚ABC与地面所成的角为

A.75° B.60° C.50° D.45°
解析:作CE⊥平面ABD于E,则∠CDE是太阳光线与地面所成的角,即∠CDE=40°,延长DE交直线AB于F,连结CF,则∠CFD是遮阳棚与地面所成的角,设为α.要使S△ABD最大,只需DF最大.在△CFD中, =
= .
.
∴DF= .
.
∵CF为定值,∴当α=50°时,DF最大.
答案:C
1.(2004年浙江,8)在△ABC中,“A>30°”是“sinA> ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:在△ABC中,A>30° 0<sinA<1sinA>
0<sinA<1sinA> ;sinA>
;sinA>
 30°<A<150°
30°<A<150° A>30°.
A>30°.
答案:B
5.在锐角△ABC中,边长a=1,b=2,则边长c的取值范围是_______.
解析:若c是最大边,则cosC>0.∴ >0,∴c<
>0,∴c< .又c>b-a=1,
.又c>b-a=1,
∴1<c< .
.
答案:(1, )
)
●典例剖析
[例1] △ABC的三个内角A、B、C的对边分别是a、b、c,如果a2=b(b+c),求证:A=2B.
剖析:研究三角形问题一般有两种思路.一是边化角,二是角化边.
证明:用正弦定理,a=2RsinA,b=2RsinB,c=2RsinC,代入a2=b(b+c)中,得sin2A=sinB(sinB+sinC) sin2A-sin2B=sinBsinC
sin2A-sin2B=sinBsinC

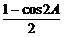 -
- =sinBsin(A+B)
=sinBsin(A+B)

 (cos2B-cos2A)=sinBsin(A+B)
(cos2B-cos2A)=sinBsin(A+B)
 sin(A+B)sin(A-B)=sinBsin(A+B),
sin(A+B)sin(A-B)=sinBsin(A+B),
因为A、B、C为三角形的三内角,所以sin(A+B)≠0.所以sin(A-B)=sinB.所以只能有A-B=B,即A=2B.
评述:利用正弦定理,将命题中边的关系转化为角间关系,从而全部利用三角公式变换求解.
思考讨论
(1)该题若用余弦定理如何解决?
解:利用余弦定理,由a2=b(b+c),得cosA= =
= =
=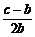 ,cos2B=2cos2B-1=2(
,cos2B=2cos2B-1=2( )2-1=
)2-1= -1=
-1=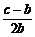 .
.
所以cosA=cos2B.因为A、B是△ABC的内角,所以A=2B.
(2)该题根据命题特征,能否构造一个符合条件的三角形,利用几何知识解决?
解:由题设a2=b(b+c),得 =
=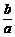 ①,
①,
作出△ABC,延长CA到D,使AD=AB=c,连结BD.①式表示的即是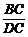 =
= ,所以△BCD∽△ABC.所以∠1=∠D.
,所以△BCD∽△ABC.所以∠1=∠D.

又AB=AD,可知∠2=∠D,所以∠1=∠2.
因为∠BAC=∠2+∠D=2∠2=2∠1,
所以A=2B.
评述:近几年的高考题中,涉及到三角形的题目,重点考查正弦、余弦定理,考查的侧重点还在于三角转换.这是命题者的初衷.
[例2] (2004年全国Ⅱ,17)已知锐角△ABC中,sin(A+B)= ,sin(A-B)=
,sin(A-B)= .
.
(1)求证:tanA=2tanB;
(2)设AB=3,求AB边上的高.
剖析:有两角的和与差联想到两角和与差的正弦公式,结合图形,以(1)为铺垫,解决(2).
(1)证明:∵sin(A+B)= ,sin(A-B)=
,sin(A-B)= ,
,
∴
 =2.
=2.
∴tanA=2tanB.
(2)解: <A+B<π,∴sin(A+B)=
<A+B<π,∴sin(A+B)= .
.
∴tan(A+B)=- ,
,
即 =-
=- .将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB=
.将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB= (负值舍去).得tanB=
(负值舍去).得tanB= ,∴tanA=2tanB=2+
,∴tanA=2tanB=2+ .
.
设AB边上的高为CD,则AB=AD+DB= +
+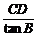 =
= .由AB=3得CD=2+
.由AB=3得CD=2+ ,所以AB边上的高为2+
,所以AB边上的高为2+ .
.
评述:本题主要考查三角函数概念,两角和与差的公式以及应用,分析和计算能力.
[例3] (2004年春季北京)在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及 的值.
的值.
剖析:因给出的是a、b、c之间的等量关系,要求∠A,需找∠A与三边的关系,故可用余弦定理.由b2=ac可变形为 =a,再用正弦定理可求
=a,再用正弦定理可求 的值.
的值.
解法一:∵a、b、c成等比数列,∴b2=ac.
又a2-c2=ac-bc,∴b2+c2-a2=bc.
在△ABC中,由余弦定理得
cosA= =
= =
= ,∴∠A=60°.
,∴∠A=60°.
在△ABC中,由正弦定理得sinB= ,
,
∵b2=ac,∠A=60°,
∴ =sin60°=
=sin60°= .
.
解法二:在△ABC中,
由面积公式得 bcsinA=
bcsinA= acsinB.
acsinB.
∵b2=ac,∠A=60°,∴bcsinA=b2sinB.
∴ =sinA=
=sinA= .
.
评述:解三角形时,找三边一角之间的关系常用余弦定理,找两边两角之间的关系常用正弦定理.
●闯关训练
夯实基础
4.已知(a+b+c)(b+c-a)=3bc,则∠A=_______.
解析:由已知得(b+c)2-a2=3bc,∴b2+c2-a2=bc.∴ =
= .∴∠A=
.∴∠A= .
.
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com