
5.如图,△ABC的BC边的中点为M,利用向量证明:AB2+AC2=2(AM2+BM2).

证明:设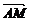 =m,
=m, =b,
=b,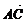 =c,则m=
=c,则m= ,m·m=
,m·m= ·
·
=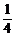 b2+
b2+ b·c+
b·c+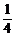 c2
c2
=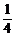 AB2+
AB2+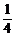 AC2+
AC2+ AB·AC·cos∠BAC
AB·AC·cos∠BAC
=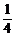 AB2+
AB2+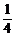 AC2+
AC2+ AB·AC·
AB·AC·
=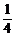 AB2+
AB2+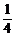 AC2+
AC2+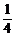 (AB2+AC2-BC2).
(AB2+AC2-BC2).
∴AM2= AB2+
AB2+ AC2-
AC2-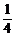 BC2.
BC2.
又∵BC2=4BM2,
∴AB2+AC2=2(AM2+BM2).
4.有一两岸平行的河流,水速为1,小船的速度为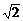 ,为使所走路程最短,小船应朝_______方向行驶.
,为使所走路程最短,小船应朝_______方向行驶.
解析:如下图,为使小船所走路程最短,v水+v船应与岸垂直.又v水= =1,v船=
=1,v船=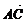 =
=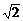 ,∠ADC=90°,∴∠CAD=45°.
,∠ADC=90°,∴∠CAD=45°.
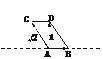
答案:与水速成135°角的
3.在一座20 m高的观测台顶测得地面一水塔塔顶仰角为60°,塔底俯角为45°,那么这座塔的高为_______.
解析:如图,AD=DC=20.
∴BD=ADtan60°=20 .
.
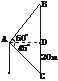
∴塔高为20(1+ ) m.
) m.
答案:20(1+ ) m
) m
2.台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A的正东40 km处,B城市处于危险区内的时间为
A.0.5 h B.1 h C.1.5 h D.2 h
解析:台风中心移动t h,城市B处在危险区,则(20t)2+402-2×20t×40×cos45°≤900.
∴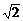 -
- ≤t≤
≤t≤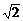 +
+ .∴B城市处在危险区的时间为1 h.
.∴B城市处在危险区的时间为1 h.
答案:B
1.(2004年辽宁,6)已知点A(-2,0),B(3,0),动点P(x,y)满足 ·
· =x2,则点P的轨迹是
=x2,则点P的轨迹是
A.圆 B.椭圆 C.双曲线 D.抛物线
解析: =(-2-x,-y),
=(-2-x,-y), =(3-x,-y),
=(3-x,-y), ·
· =(-2-x)(3-x)+(-y)2=x2,整理得y2=x+6.∴P点的轨迹为抛物线.
=(-2-x)(3-x)+(-y)2=x2,整理得y2=x+6.∴P点的轨迹为抛物线.
答案:D
5.(2004年全国Ⅱ,理9)已知平面上直线l的方向向量e=(- ,
, ),点O(0,0)和A(1,-2)在l上的射影分别是
),点O(0,0)和A(1,-2)在l上的射影分别是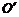 和A′,则
和A′,则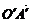 =λe,其中λ等于
=λe,其中λ等于
A. B.-
B.- C.2 D.-2
C.2 D.-2
解析:如图所示,令e过原点,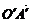 与e方向相反,排除A、C,验证D即可.
与e方向相反,排除A、C,验证D即可.

答案:D
●典例剖析
[例1] 已知a、b是两个非零向量,当a+tb(t∈R)的模取最小值时,
(1)求t的值;
(2)求证:b⊥(a+tb).
剖析:利用|a+tb|2=(a+tb)2进行转换,可讨论有关|a+tb|的最小值问题,若能计算得b·(a+tb)=0,则证得了b⊥(a+tb).
(1)解:设a与b的夹角为θ,则
|a+tb|2=(a+tb)2=|a|2+t2|b|2+2a·(tb)=|a|2+t2|b|2+2t|a||b|cosθ=|b|2(t+ cosθ)2+|a|2sin2θ,
cosθ)2+|a|2sin2θ,
所以当t=- cosθ=-
cosθ=-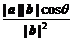 =-
=-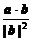 时,|a+tb|有最小值.
时,|a+tb|有最小值.
(2)证明:因为b·(a+tb)=b·(a-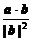 ·b)=a·b-a·b=0,所以b⊥(a⊥tb).
·b)=a·b-a·b=0,所以b⊥(a⊥tb).
评注:用向量的数量积可以处理有关长度、角度和垂直等几何问题,向量的坐标运算为处理这类问题带来了很大的方便.
思考讨论
对|a+tb|的变形,有两种基本的思考方法:一是通过|a+tb|2=(a+tb)2进行向量的数量积运算;二是设a、b的坐标,通过向量的坐标运算进行有目的的变形.读者可尝试用后一方法解答本题.
深化拓展
已知 =a,
=a,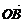 =b,a·b=|a-b|=2,当△AOB面积取最大值时,求a与b的夹角.
=b,a·b=|a-b|=2,当△AOB面积取最大值时,求a与b的夹角.
解:因为|a-b|2=4,所以a2-2a·b+b2=4.所以|a|2+|b|2=4+2a·b=8,
S△AOB=
 ·
·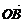 sinθ
sinθ
= |a||b|
|a||b|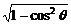
=

=
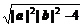
≤
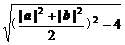 =
= ,
,
(当且仅当|a|=|b|=2时取等号)
所以当|a|=|b|=2时,△AOB的面积取最大值,这时,cosθ=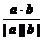 =
= =
= ,所以θ=60°.
,所以θ=60°.
[例2] 如图,四边形MNPQ是⊙C的内接梯形,C是圆心,C在MN上,向量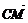 与
与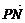 的夹角为120°,
的夹角为120°,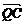 ·
·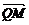 =2.
=2.
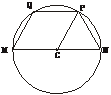
(1)求⊙C的方程;
(2)求以M、N为焦点且过点P、Q的椭圆的方程.
剖析:需先建立直角坐标系,为了使所求方程简单,需以C为原点,MN所在直线为x轴,求⊙C的方程时,只要求半径即可,求椭圆的方程时,只需求a、b即可.
解:(1)以MN所在直线为x轴,C为原点,建立直角坐标系xOy.∵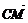 与
与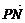 的夹角为120°,故∠QCM=60°.于是△QCM为正三角形,∠CQM=60°.
的夹角为120°,故∠QCM=60°.于是△QCM为正三角形,∠CQM=60°.
又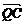 ·
·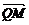 =2,即|
=2,即|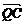 ||
||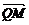 |cos∠CQM=2,于是r=|
|cos∠CQM=2,于是r=|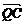 |=2.
|=2.
故⊙C的方程为x2+y2=4.
(2)依题意2c=4,2a=|QN|+|QM|,
而|QN|=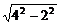 =2
=2 ,|QM|=2,
,|QM|=2,
于是a= +1,b2=a2-c2=2
+1,b2=a2-c2=2 .
.
∴所求椭圆的方程为 +
+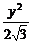 =1.
=1.
评述:平面向量在解析几何中的应用越来越广,复习时应引起重视.
●闯关训练
夯实基础
4.在四边形ABCD中, ·
· =0,
=0, =
= ,则四边形ABCD是
,则四边形ABCD是
A.直角梯形 B.菱形 C.矩形 D.正方形
解析:由 ·
· =0知
=0知 ⊥
⊥ .由
.由 =
= 知BC
知BC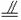 AD.∴四边形ABCD是矩形.
AD.∴四边形ABCD是矩形.
答案:C
3.平面直角坐标系中,O为坐标原点,已知两点A(3,1)、B(-1,3),若点C满足 =α
=α +β
+β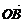 ,其中α、β∈R,且α+β=1,则点C的轨迹方程为
,其中α、β∈R,且α+β=1,则点C的轨迹方程为
A.3x+2y-11=0 B.(x-1)2+(y-2)2=5
C.2x-y=0 D.x+2y-5=0
解析:C点满足 =α
=α +β
+β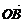 且α+β=1,∴A、B、C三点共线.∴C点的轨迹是直线AB.
且α+β=1,∴A、B、C三点共线.∴C点的轨迹是直线AB.
答案:D
2.将椭圆x2+6y2-2x-12y-13=0按向量a平移,使中心与原点重合,则a的坐标是
A.(-1,1) B.(1,-1)
C.(-1,-1) D.(1,1)
解析:椭圆方程变形为(x-1)2+6(y-1)2=20.
需按a=(-1,-1)平移,中心与原点重合.
答案:C
1.若O是△ABC内一点, +
+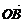 +
+ =0,则O是△ABC的
=0,则O是△ABC的
A.内心 B.外心 C.垂心 D.重心
解析:以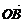 、
、 为邻边作平行四边形OBDC,则
为邻边作平行四边形OBDC,则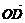 =
=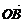 +
+ .
.

又 +
+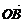 +
+ =0,
=0,
∴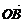 +
+ =-
=- .
.
∴- =
=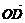 .∴O为AD的中点,且A、O、D共线.
.∴O为AD的中点,且A、O、D共线.
又E为OD的中点,∴O是中线AE的三等分点,且OA=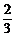 AE.
AE.
∴O是△ABC的重心.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com