
3.要注意不等式性质成立的条件.例如,重要结论:a>b,ab>0
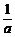 <
< ,不能弱化条件得a>b
,不能弱化条件得a>b
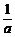 <
< ,也不能强化条件得a>b>0
,也不能强化条件得a>b>0
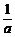 <
< .
.
2.基本性质:(1)a>b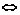 b<a.
b<a.
(2)a>b,b>c a>c.
a>c.
(3)a>b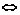 a+c>b+c;a>b,c>d
a+c>b+c;a>b,c>d a+c>b+d.
a+c>b+d.
(4)a>b,c>0 ac>bc;a>b,c<0
ac>bc;a>b,c<0 ac<bc;
ac<bc;
a>b>0,c>d>0 ac>bd.
ac>bd.
(5)a>b>0
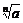 >
> (n∈N,n>1);
(n∈N,n>1);
a>b>0 an>bn(n∈N,n>1).
an>bn(n∈N,n>1).
1.比较准则:a-b>0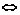 a>b;
a>b;
a-b=0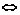 a=b;a-b<0
a=b;a-b<0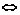 a<b.
a<b.
6.1 不等式的性质
●知识梳理
7.要强化不等式的应用意识,同时要注意到不等式与函数方程的对比与联系.
6.对于含有绝对值的不等式(问题),要紧紧抓住绝对值的定义实质,充分利用绝对值的几何意义.
5.利用平均值定理解决问题时,要注意满足定理成立的三个条件:一“正”、二“定”、三“相等”.
4.注意重要不等式和常用思想方法在解题中的作用.
3.解(证)某些不等式时,要把函数的定义域、值域和单调性结合起来.
2.不等式的证明方法除比较法、分析法、综合法外,还有反证法、换元法、判别式法、构造法、几何法,这些方法可作了解,但要控制量和度,切忌喧宾夺主.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com