2.该类问题用线性规划能解吗?并试着解决如下问题：

已知函数f(x)=ax²－c，满足－4≤f(1)≤－1，－1≤f(2)≤5，求f(3)的最大值和最小值.

答案：20　 －1

[例2] (2004年福建，3)命题p：若a、b∈R，则|a|+|b|＞1是|a+b|＞1的充分而不必要条件；命题q：函数y=的定义域是(－∞，－1］∪［3，+∞)，则

A.“p或q”为假　　　　　　　　　　　　　　　　　　　　　　 B.“p且q”为真

C. p真q假　　　　　　　　　　　　　　　　　　　　　　　　　　 D. p假q真

剖析：只需弄清命题p、q的真假即可.

解：∵|a+b|≤|a|+|b|，若|a|+|b|＞1不能推出|a+b|＞1，

而|a+b|＞1一定有|a|+|b|＞1，故命题p为假.

又函数y=的定义域为|x－1|－2≥0，∴|x－1|≥2.

∴x≤－1或x≥3.∴q为真.

答案：D

[例3] 比较1+log_x3与2log_x2(x＞0且x≠1)的大小.

剖析：由于要比较的两个数都是对数，我们联系到对数的性质，以及对数函数的单调性.

解：(1+log_x3)－2log_x2=log_x.

当或

即0＜x＜1或x＞时，

有log_x＞0，1+log_x3＞2log_x2.

当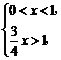①或②时，log_x＜0.

解①得无解，解②得1＜x＜，

即当1＜x＜时，有log_x＜0，

1+log_x3＜2log_x2.

当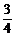x=1，即x=时，有log_x=0.

∴1+log_x3=2log_x2.

综上所述，当0＜x＜1或x＞时，1+log_x3＞2log_x2；

当1＜x＜时，1+log_x3＜2log_x2；

当x=时，1+log_x3=2log_x2.

评述：作差看符号是比较两数大小的常用方法，在分类讨论时，要做到不重复、不遗漏.

深化拓展

函数f(x)=x²+(b－1)x+c的图象与x轴交于(x₁，0)、(x₂，0)，且x₂－x₁＞1.当t＜x₁时，比较t²+bt+c与x₁的大小.

提示：令f(x)=(x－x₁)(x－x₂)，

∴x²+bx+c=(x－x₁)(x－x₂)+x.

把t²+bt+c与x₁作差即可.

答案：t²+bt+c＞x₁.

●闯关训练

夯实基础

1.评述中解法错在何处?

5.设a=2－，b=－2，c=5－2，则a、b、c之间的大小关系为____________.

解析：a=2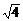－=－＜0，∴b＞0.

c=5－2=－＞0.

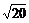b－c=3－7=－＜0.

∴c＞b＞a.

答案：c＞b＞a

●典例剖析

[例1] 已知－1＜a+b＜3且2＜a－b＜4，求2a+3b的取值范围.

剖析：∵a+b，a－b的范围已知，

∴要求2a+3b的取值范围，

只需将2a+3b用已知量a+b，a－b表示出来.

可设2a+3b=x(a+b)+y(a－b)，用待定系数法求出x、y.

解：设2a+3b=x(a+b)+y(a－b)，

∴解得

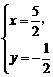
∴－＜(a+b)＜，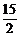

－2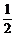＜－(a－b)＜－1.

∴－＜(a+b)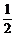－(a－b)＜，

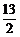即－＜2a+3b＜.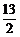

评述：解此题常见错误是：－1＜a+b＜3，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

2＜a－b＜4.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

①+②得1＜2a＜7.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

由②得－4＜b－a＜－2.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

①+④得－5＜2b＜1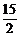，∴－＜3b＜.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

③+⑤得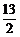－＜2a+3b＜.

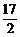思考讨论

4.a＞b＞0，m＞0，n＞0，则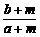，，，的由大到小的顺序是____________.

解析：特殊值法即可

答案：＞＞＞

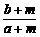3.设α∈(0，)，β∈［0，］，那么2α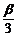－的范围是

A.(0，)　　　　　　　　　　　　　　　　　　　　　　　　 B.(－，)

C.(0，π)　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－，π)

解析：由题设得0＜2α＜π，0≤≤.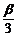

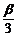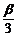∴－≤－≤0.∴－＜2α－＜π.

答案：D

2.(2004年春季北京，7)已知三个不等式：ab＞0，bc－ad＞0，－＞0(其中a、b、c、d均为实数)，用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题的个数是

A.0　　　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　　 C.2　　　　　　　　　　　　　　　 D.3

解析：由ab＞0，bc－ad＞0可得出

－＞0.

bc－ad＞0，两端同除以ab，得－＞0.

同样由－＞0，ab＞0可得bc－ad＞0.

ab＞0.

答案：D

1.若a＜b＜0，则下列不等式不能成立的是

A.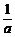＞　　　 　　　　　　　　　　　　　　　　　　　　　　　　 B.2^a＞2^b

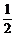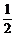C.|a|＞|b|　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.()^a＞()^b

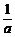解析：由a＜b＜0知ab＞0，因此a·＜b·，即＞成立；

由a＜b＜0得－a＞－b＞0，因此|a|＞|b|＞0成立.

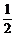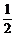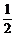又()^x是减函数，所以()^a＞()^b成立.

故不成立的是B.

答案：B

6.性质(5)中的指数n可以推广到任意正数的情形.

特别提示

不等式的性质从形式上可分两类：一类是“”型；另一类是“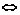”型.要注意二者的区别.

●点击双基

5.性质(3)的推论以及性质(4)的推论可以推广到两个以上的同向不等式.

4.要正确处理带等号的情况.如由a＞b，b≥c或a≥b，b＞c均可得出a＞c；而由a≥b，b≥c可能有a＞c，也可能有a=c，当且仅当a=b且b=c时，才会有a=c.