
1.不等式的性质是解、证不等式的基础,对任意两实数a、b有a-b>0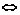 a>b,a-b=0
a>b,a-b=0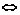 a=b,a-b<0
a=b,a-b<0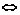 a<b,这是比较两数(式)大小的理论根据,也是学习不等式的基石.
a<b,这是比较两数(式)大小的理论根据,也是学习不等式的基石.
9.已知x>-1,n≥2且n∈N*,比较(1+x)n与1+nx的大小.
解:设f(x)=(1+x)n-(1+nx),
则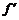 (x)=n(1+x)n-1-n=n[(1+x)n-1-1].
(x)=n(1+x)n-1-n=n[(1+x)n-1-1].
由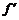 (x)=0得x=0.
(x)=0得x=0.
当x∈(-1,0)时,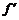 (x)<0,
(x)<0,
f(x)在(-1,0)上递减.
当x∈(0,+∞)时,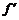 (x)>0,
(x)>0,
f(x)在(0,+∞)上递增.
∴x=0时,f(x)最小,最小值为0,即f(x)≥0.
∴(1+x)n≥1+nx.
评述:理科学生也可以用数学归纳法证明.
●思悟小结
8.设a1≈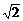 ,令a2=1+
,令a2=1+ .
.
(1)证明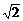 介于a1、a2之间;
介于a1、a2之间;
(2)求a1、a2中哪一个更接近于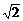 ;
;
(3)你能设计一个比a2更接近于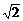 的一个a3吗?并说明理由.
的一个a3吗?并说明理由.
(1)证明:(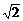 -a1)(
-a1)(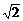 -a2)=(
-a2)=(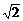 -a1)·
(
-a1)·
(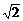 -1-
-1- )=
)=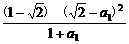 <0.
<0.
∴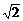 介于a1、a2之间.
介于a1、a2之间.
(2)解:|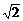 -a2|=|
-a2|=|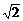 -1-
-1- |
|
=| |
|
= |
|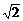 -a1|<|
-a1|<|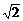 -a1|.
-a1|.
∴a2比a1更接近于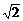 .
.
(3)解:令a3=1+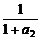 ,
,
则a3比a2更接近于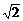 .
.
由(2)知|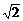 -a3|=
-a3|= |
|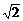 -a2|<|
-a2|<|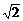 -a2|.
-a2|.
探究创新
7.设0<x<1,a>0且a≠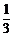 ,试比较|log3a(1-x)3|与|log3a(1+x)3|的大小.
,试比较|log3a(1-x)3|与|log3a(1+x)3|的大小.
解:∵0<x<1,∴①当3a>1,即a>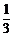 时,
时,
|log3a(1-x)3|-|log3a(1+x)3|
=|3log3a(1-x)|-|3log3a(1+x)|
=3[-log3a(1-x)-log3a(1+x)]
=-3log3a(1-x2).
∵0<1-x2<1,∴-3log3a(1-x2)>0.
②当0<3a<1,即0<a<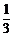 时,
时,
|log3a(1-x)3|-|log3a(1+x)3|
=3[log3a(1-x)+log3a(1+x)]
=3log3a(1-x2)>0.
综上所述,|log3a(1-x)3|>|log3a(1+x)3|.
6.设A=xn+x-n,B=xn-1+x1-n,当x∈R+,n∈N时,求证:A≥B.
证明:A-B=(xn+x-n)-(xn-1+x1-n)
=x-n(x2n+1-x2n-1-x)
=x-n[x(x2n-1-1)-(x2n-1-1)]
=x-n(x-1)(x2n-1-1).
由x∈R+,x-n>0,得
当x≥1时,x-1≥0,x2n-1-1≥0;
当x<1时,x-1<0,x2n-1<0,即
x-1与x2n-1-1同号.∴A-B≥0.∴A≥B.
培养能力
5.已知a>2,b>2,试比较a+b与ab的大小.
解:∵ab-(a+b)=(a-1)(b-1)-1,
又a>2,b>2,∴a-1>1,b-1>1.
∴(a-1)(b-1)>1,(a-1)(b-1)-1>0.
∴ab>a+b.
4.若1<α<3,-4<β<2,则α-|β|的取值范围是____________.
解析:∵-4<β<2,∴0≤|β|<4.
∴-4<-|β|≤0.∴-3<α-|β|<3.
答案:(-3,3)
3.已知-1<2a<0,A=1+a2,B=1-a2,C=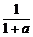 ,D=
,D=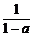 则A、B、C、D按从小到大的顺序排列起来是____________.
则A、B、C、D按从小到大的顺序排列起来是____________.
解析:取特殊值a=-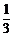 ,计算可得A=
,计算可得A= ,B=
,B=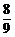 ,C=
,C= ,D=
,D=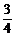 .
.
∴D<B<A<C.
答案:D<B<A<C
2.若p=a+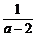 (a>2),q=2
(a>2),q=2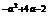 ,则
,则
A.p>q B.p<q C.p≥q D.p≤q
解析:p=a-2+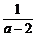 +2≥4,而-a2+4a-2=-(a-2)2+2<2,∴q<4.∴p>q.
+2≥4,而-a2+4a-2=-(a-2)2+2<2,∴q<4.∴p>q.
答案:A
1.(2004年辽宁,2)对于0<a<1,给出下列四个不等式:
①loga(1+a)<loga(1+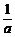 );②loga(1+a)>loga(1+
);②loga(1+a)>loga(1+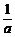 );③a1+a<a1
);③a1+a<a1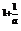 ;④a1+a>a
;④a1+a>a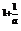 .其中成立的是
.其中成立的是
A.①③ B.①④ C.②③ D.②④
解析:∵0<a<1,∴a<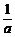 ,从而1+a<1+
,从而1+a<1+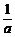 .
.
∴loga(1+a)>loga(1+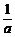 ).
).
又∵0<a<1,∴a1+a>a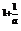 .
.
故②与④成立.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com