
3.设a>0,b>0,a2+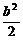 =1,则a
=1,则a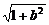 的最大值是____________.
的最大值是____________.
解析:a2+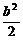 =1
=1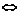 a2+
a2+ =
=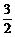 .
.
∴a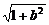 =
=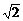 ·a·
·a·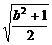 ≤
≤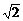 ·
·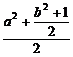 =
=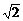 ·
· =
=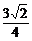 .
.
答案: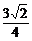
2.已知x、y∈R,M=x2+y2+1,N=x+y+xy,则M与N的大小关系是
A.M≥N B.M≤N C.M=N D.不能确定
解析:M-N=x2+y2+1-(x+y+xy)
=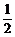 [(x2+y2-2xy)+(x2-2x+1)+(y2-2y+1)]
[(x2+y2-2xy)+(x2-2x+1)+(y2-2y+1)]
=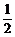 [(x-y)2+(x-1)2+(y-1)2]≥0.
[(x-y)2+(x-1)2+(y-1)2]≥0.
答案:A
1.设x>0,y>0,且xy-(x+y)=1,则
A.x+y≤2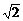 +2 B.x+y≥2
+2 B.x+y≥2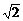 +2
+2
C.x+y≤(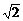 +1)2 D.x+y≥(
+1)2 D.x+y≥(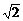 +1)2
+1)2
解析:∵x>0,y>0,∴xy≤(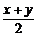 )2.
)2.
由xy-(x+y)=1得(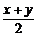 )2-(x+y)≥1.
)2-(x+y)≥1.
∴x+y≥2+2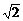 .
.
答案:B
5.船在流水中在甲地和乙地间来回行驶一次的平均速度v1和在静水中的速度v2的大小关系为____________.
解析:设甲地至乙地的距离为s,船在静水中的速度为v2,水流速度为v(v2>v>0),则船在流水中在甲乙间来回行驶一次的时间
t=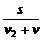 +
+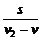 =
=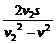 ,
,
平均速度v1= =
= .
.
∵v1-v2= -v2=-
-v2=-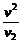 <0,
<0,
∴v1<v2.
答案:v1<v2
●典例剖析
[例1] 设a>0,b>0,求证:(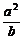 )
)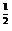 (
( )
)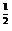 ≥a
≥a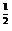 +b
+b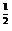 .
.
剖析:不等式两端都是多项式的形式,故可用比差法证明或比商法证明.
证法一:左边-右边=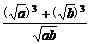 -(
-(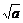 +
+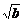 )
)
=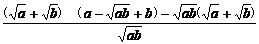
=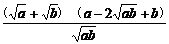 =
=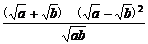 ≥0.
≥0.
∴原不等式成立.
证法二:左边>0,右边>0,
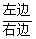 =
=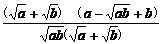 =
= ≥
≥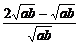 =1.
=1.
∴原不等式成立.
评述:用比较法证不等式,一般要经历作差(或商)、变形、判断三个步骤.变形的主要手段是通分、因式分解或配方.在变形过程中,也可利用基本不等式放缩,如证法二.下面的例3则是公式法与配方法的综合应用.
[例2] 已知a、b、x、y∈R+且 >
>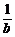 ,x>y.
,x>y.
求证: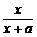 >
>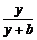 .
.
剖析:观察待证不等式的特征,用比较法或分析法较适合.
证法一:(作差比较法)
∵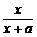 -
-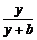 =
= ,
,
又 >
>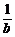 且a、b∈R+,
且a、b∈R+,
∴b>a>0.又x>y>0,∴bx>ay.
∴ >0,即
>0,即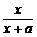 >
>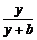 .
.
证法二:(分析法)
∵x、y、a、b∈R+,∴要证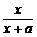 >
>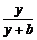 ,
,
只需证明x(y+b)>y(x+a),即证xb>ya.
而由 >
>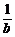 >0,∴b>a>0.又x>y>0,
>0,∴b>a>0.又x>y>0,
知xb>ya显然成立.故原不等式成立.
思考讨论
该例若用函数的单调性应如何构造函数?
解法一:令f(x)=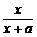 ,易证f(x)在(0,+∞)上为增函数,从而
,易证f(x)在(0,+∞)上为增函数,从而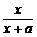 >
>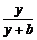 .
.
再令g(x)=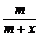 ,易证g(x)在(0,+∞)上单调递减.
,易证g(x)在(0,+∞)上单调递减.
∵ >
>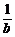 ,a、b∈R+.∴a<b.
,a、b∈R+.∴a<b.
∴g(a)>g(b),即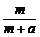 >
>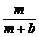 ,命题得证.
,命题得证.
解法二:原不等式即为 >
>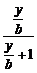 ,
,
为此构造函数f(x)=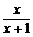 ,x∈(0,+∞).
,x∈(0,+∞).
易证f(x)在(0,+∞)上为单调增函数,而 >
>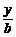 ,
,
∴ >
>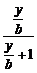 ,即
,即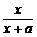 >
>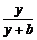 .
.
[例3] 某食品厂定期购买面粉.已知该厂每天需用面粉6 t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210 t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由.
解:(1)设该厂应每隔x天购买一次面粉,其购买量为6x t,由题意知,面粉的保管等其他费用为3[6x+6(x-1)+…+6×2+6×1]=9x(x+1).
设平均每天所支付的总费用为y1元,则y1=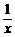 [9x(x+1)+900]+6×1800
[9x(x+1)+900]+6×1800
=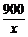 +9x+10809≥2
+9x+10809≥2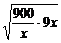 +10809
+10809
=10989.
当且仅当9x=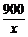 ,即x=10时取等号,
,即x=10时取等号,
即该厂应每隔10天购买一次面粉,才能使平均每天所支付的总费用最少.
(2)若厂家利用此优惠条件,则至少每隔35天,购买一次面粉,平均每天支付的总费用为y2元,则
y2=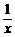 [9x(x+1)+900]+6×1800×0.90
[9x(x+1)+900]+6×1800×0.90
=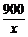 +9x+9729(x≥35).
+9x+9729(x≥35).
令f(x)=x+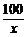 (x≥35),
(x≥35),
x2>x1≥35,则
f(x1)-f(x2)=(x1+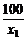 )-(x2+
)-(x2+ )
)
=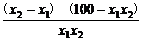
∵x2>x1≥35,
∴x2-x1>0,x1x2>0,100-x1x2<0.
∴f(x1)-f(x2)<0,f(x1)<f(x2),
即f(x)=x+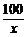 ,当x≥35时为增函数.
,当x≥35时为增函数.
∴当x=35时,f(x)有最小值,此时y2<10989.∴该厂应该接受此优惠条件.
●闯关训练
夯实基础
4.(理)已知|a+b|<-c(a、b、c∈R),给出下列不等式:
①a<-b-c;②a>-b+c;③a<b-c;④|a|<|b|-c;⑤|a|<-|b|-c.
其中一定成立的不等式是____________.(把成立的不等式的序号都填上)
解析:∵|a+b|<-c,∴c<a+b<-c.
∴-b+c<a<-b-c.故①②成立,③不成立.
∵|a+b|<-c,|a+b|≥|a|-|b|,
∴|a|-|b|<-c.∴|a|<|b|-c.
故④成立,⑤不成立.
答案:①②④
(文)若a、b∈R,有下列不等式:①a2+3>2a;②a2+b2≥2(a-b-1);③a5+b5>a3b2+a2b3;④a+ ≥2.其中一定成立的是__________.
≥2.其中一定成立的是__________.
解析:①a2+3-2a=(a-1)2+2>0,
∴a2+3>2a;
②a2+b2-2a+2b+2=(a-1)2+(b+1)2≥0,
∴a2+b2≥2(a-b-1);
③a5+b5-a3b2-a2b3=a3(a2-b2)+b3(b2-a2)
=(a2-b2)(a3-b3)=(a+b)(a-b)2(a2+ab+b2).
∵(a-b)2≥0,a2+ab+b2≥0,但a+b符号不确定,
∴a5+b5>a3b2+a2b3不正确;
④a∈R时,a+ ≥2不正确.
≥2不正确.
答案:①②
3.(2005年春季上海,15)若a、b、c是常数,则“a>0且b2-4ac<0”是“对任意x∈R,有ax2+bx+c>0”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 必要条件
解析:当a>0,b2-4ac<0时,ax2+bx+c>0.
反之,ax2+bx+c>0对x∈R成立不能推出a>0,b2-4ac<0.
反例:a=b=0,c=2.故选A.
答案:A
2.设0<x<1,则a=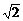 x,b=1+x,c=
x,b=1+x,c=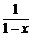 中最大的一个是
中最大的一个是
A.a B.b C.c D.不能确定
解析:∵0<x<1,
∴1+x>2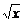 =
=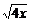 >
>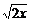 .
.
∴只需比较1+x与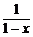 的大小.
的大小.
∵1+x-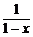 =
=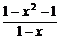 =-
=-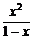 <0,
<0,
∴1+x<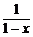 .
.
答案:C
1.若a、b是正数,则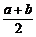 、
、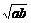 、
、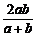 、
、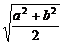 这四个数的大小顺序是
这四个数的大小顺序是
A.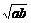 ≤
≤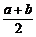 ≤
≤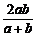 ≤
≤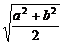
B.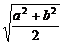 ≤
≤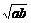 ≤
≤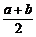 ≤
≤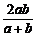
C.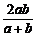 ≤
≤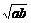 ≤
≤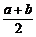 ≤
≤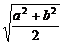
D.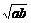 ≤
≤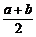 ≤
≤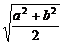 ≤
≤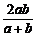
解析:可设a=1,b=2,
则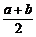 =
=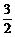 ,
,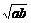 =
=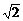 ,
,
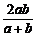 =
=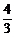 ,
,
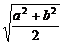 =
=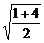 =
=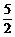 =
=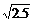 .
.
答案:C
2.比商法要注意使用条件,若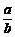 >1不能推出a>b.这里要注意a、b两数的符号.
>1不能推出a>b.这里要注意a、b两数的符号.
●点击双基
1.比较法证明不等式是不等式证明的最基本的方法.作差后需要判断差的符号,作差变形的方向常常是因式分解后,把差写成积的形式或配成完全平方式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com