
4.在应用均值定理求最值时,要把握定理成立的三个条件,就是“一正--各项均为正;二定--积或和为定值;三相等--等号能否取得”.若忽略了某个条件,就会出现错误.
●教师下载中心
教学点睛
3.有时要先对不等式作等价变形再进行证明,有时几种证明方法综合使用.
2.步骤是:作差(商)→变形→判断.变形的目的是为了判断.若是作差,就判断与0的大小关系,为了便于判断,往往把形式变为积或完全平方式.若是作商,两边为正,就判断与1的大小关系.
1.比较法有两种形式:一是作差,二是作商.用作差法证明不等式是证明不等式中最基本、最常用的方法.它的依据是不等式的基本性质.
9.设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两根x1、x2满足1<x1<x2<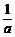 .
.
(1)当x∈(0,x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称,求证x0<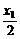 .
.
证明:(1)令F(x)=f(x)-x,
∵x1、x2是方程f(x)-x=0的根,
∴F(x)=a(x-x1)(x-x2).
当x∈(0,x1)时,由于x1<x2,
∴(x-x1)(x-x2)>0.
又a>0,得F(x)=a(x-x1)(x-x2)>0,
即x<f(x).
又x1-f(x)=x1-[x+F(x)]=x1-x+a(x1-x)(x-x2)=(x1-x)[1+a(x-x2)],
∵0<x<x1<x2<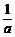 ,x1-x>0,
,x1-x>0,
1+a(x-x2)=1+ax-ax2>1-ax2>0,
∴x1-f(x)>0,即f(x)<x1.
综上,可知x<f(x)<x1.
(2)由题意知x0=-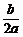 .
.
∵x1、x2是方程f(x)-x=0的根,
即x1、x2是方程ax2+(b-1)x+c=0的根,
∴x1+x2=-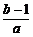 .
.
∴x0=-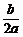 =
=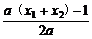 =
=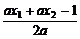 .
.
又∵ax2<1,∴x0<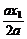 =
=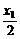 .
.
●思悟小结
8.有点难度哟!
求证:在非Rt△ABC中,若a>b,ha、hb分别表示a、b边上的高,则必有a+ha>b+hb.
证明:设S表示△ABC的面积,则
S= aha=
aha= bhb=
bhb= absinC.
absinC.
∴ha=bsinC,hb=asinC.
∴(a+ha)-(b+hb)=a+bsinC-b-asinC
=(a-b)(1-sinC).
∵C≠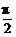 ,∴1-sinC>0.
,∴1-sinC>0.
∴(a-b)(1-sinC)>0.
∴a+ha>b+hb.
探究创新
7.已知x>0,y>0,若不等式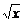 +
+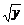 ≤m
≤m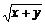 恒成立,求实数m的最小值.
恒成立,求实数m的最小值.
分析:∵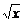 +
+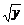 ≤m
≤m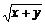 恒成立,
恒成立,
∴m≥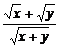 恒成立.
恒成立.
∴m的最小值就是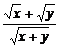 的最大值.
的最大值.
解:∵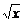 +
+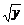 ≤m
≤m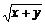 恒成立,
恒成立,
∴m≥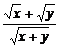 恒成立.
恒成立.
∵x>0,y>0,
∴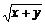 ≥
≥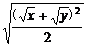 =
=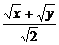 .
.
∴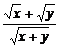 ≤
≤ =
= .
.
∴m的最小值为 .
.
评述:分离参数法是求参数的范围问题常用的方法,化归是解这类问题常用的手段.
6.已知a>1,λ>0,求证:loga(a+λ)>loga+λ(a+2λ).
证明:loga(a+λ)-log(a+λ)(a+2λ)
=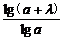 -
-
=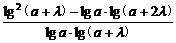
∵a>1,λ>0,
∴lga>0,lg(a+2λ)>0,且lga≠lg(a+2λ).
∴lga·lg(a+2λ)<[(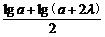 )]2
)]2
=[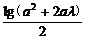 ]2<[
]2<[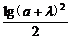 ]2=lg2(a+λ).
]2=lg2(a+λ).
∴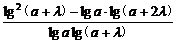 >0.
>0.
∴loga(a+λ)>log(a+λ)(a+2λ).
培养能力
5.当m>n时,求证:m3-m2n-3mn2>2m2n-6mn2+n3.
证明:∵(m3-m2n-3mn2)-(2m2n-6mn2+n3)=m3-3m2n+3mn2-n3=(m-n)3,
又m>n,∴m-n>0.∴(m-n)3>0,
即(m3-m2n-3mn2)-(2m2n-6mn2+n3)>0.
故m3-m2n-3mn2>2m2n-6mn2+n3.
4.若记号“※”表示求两个实数a和b的算术平均数的运算,即a※b= ,则两边均含有运算符号“※”和“+”,且对于任意3个实数a、b、c都能成立的一个等式可以是____________.
,则两边均含有运算符号“※”和“+”,且对于任意3个实数a、b、c都能成立的一个等式可以是____________.
解析:∵a※b= ,b※a=
,b※a= ,
,
∴a※b+c=b※a+c.
答案:a※b+c=b※a+c.
思考:对于运算“※”分配律成立吗?
即a※(b+c)=a※b+a※c.
答案:不成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com