7.反证法、换元法等.

特别提示

不等式证明方法多，证法灵活，其中比较法、分析法、综合法是基本方法，要熟练掌握，其他方法作为辅助，这些方法之间不能截然分开，要综合运用各种方法.

●点击双基

6.数形结合法证明不等式.

5.构造一元二次方程利用“Δ”法证明不等式.

4.利用单调性证明不等式.

3.放缩法证明不等式.

2.用分析法证明不等式：从待证不等式出发，分析并寻求使这个不等式成立的充分条件的方法叫分析法，概括为“执果索因”.

1.用综合法证明不等式：利用不等式的性质和已证明过的不等式以及函数的单调性导出待证不等式的方法叫综合法，概括为“由因导果”.

6.3　 不等式的证明(二)

●知识梳理

2.对于公式a+b≥2，ab≤()²要讲清它们的作用和使用条件及内在联系，两个公式也体现了ab和a+b的转化关系.

拓展题例

[例1]设a、b∈R，关于x的方程x²+ax+b＝0的实根为α、β.若｜a｜+｜b｜＜1，求证：｜α｜＜1，｜β｜＜1.

证法一：∵α+β＝－a，αβ＝b，

∴｜α+β｜+｜αβ｜＝｜a｜+｜b｜＜1.

∴｜α｜－｜β｜+｜α｜｜β｜＜1，(｜α｜－1)(｜β｜+1)＜0.

∴｜α｜＜1.同理，｜β｜＜1.

证法二：设f(x)=x²+ax+b，则有

f(1)＝1+a+b＞1－(｜a｜+｜b｜)＞1－1＝0，

f(－1)＝1－a+b＞1－(｜a｜+｜b｜)＞0.

∵0≤｜a｜＜1，∴－1＜a＜1.

∴－＜－＜.

∴方程f(x)＝0的两实根在(－1，1)内，即｜α｜＜1，｜β｜＜1.

评述：证法一先利用韦达定理，再用绝对值不等式的性质恰好能分解因式；证法二考虑根的分布，证两根在(－1，1)内.

[例2] 是否存在常数C，使得不等式+≤C≤+对任意正数x、y恒成立?试证明你的结论.

解：当x=y时，可由不等式得出C=.

下面分两个方面证明.

先证+≤，此不等式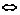3x(x+2y)+3y(2x+y)≤2(2x+y)(x+2y)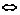x²+y²≥2xy.

再证+≥，

此不等式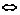3x(2x+y)+3y(x+2y)≥2(x+2y)(2x+y)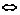2xy≤x²+y².

综上，可知存在常数C=，使对任何正数x、y不等式恒成立.

1.在证明不等式的各种方法中，作差比较法是一种最基本、最重要的方法，它是利用不等式两边的差是正数还是负数来证明不等式，其应用非常广泛，一定要熟练掌握.