
2.不等式应用大致可分为两类:一类是建立不等式参数的取值范围或解决一些实际应用问题;另一类是建立函数关系,利用均值不等式求最值问题.
1.不等式的实际应用,题源丰富,综合性强,是高考应用题命题的重点内容之一.不等式应用题大都是以函数的面目出现,以最优化的形式展现.在解题过程中涉及均值不等式,常常与集合问题,方程(组)解的讨论,函数定义域、值域的确定,函数单调性的研究,三角、数列、立体几何中的最值问题,解析几何中的直线与圆锥曲线位置关系的讨论等等有着密切的关系.
9.有点难度哟!
已知函数f(x)满足2axf(x)=2f(x)-1,f(1)=1,设无穷数列{an}满足an+1=f(an).
(1)求函数f(x)的表达式;
(2)若a1=3,从第几项起,数列{an}中的项满足an<an+1;
(3)若1+ <a1<
<a1<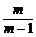 (m为常数且m∈N,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立.
(m为常数且m∈N,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立.
解:(1)令x=1得2a=1,∴a= .
.
∴f(x)= .
.
(2)若a1=3,由a2=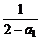 =-1,a3=
=-1,a3= =
=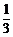 ,a4=
,a4=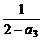 =
= ,
,
假设当n≥3时,0<an<1,则0<an+1=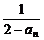 <
< =1
=1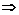 2-an>0.
2-an>0.
从而an+1-an=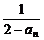 -an=
-an= >0
>0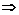 an+1>an.
an+1>an.
从第2项起,数列{an}满足an<an+1.
(3)当1+ <a1<
<a1<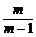 时,a2=
时,a2=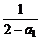 ,得
,得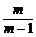 <a2<
<a2< .
.
同理, <a3<
<a3<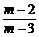 .
.
假设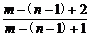 <an-1<
<an-1<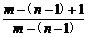 .
.
由an= 与归纳假设知
与归纳假设知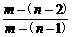 <an<
<an< 对n∈N*都成立.
对n∈N*都成立.
当n=m时,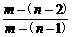 <am,即am>2.
<am,即am>2.
∴am+1=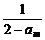 <0.
<0.
0<am+2=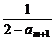 <
< <1.
<1.
由(2)证明知若0<an<1,则0<an+1=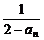 <
< =1.
=1.
∴N=m+2,使得n≥N时总有0<an<1成立.
●思悟小结
8.设f(x)=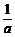 x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
解:∵f(x)<0的解集是(-1,3),
∴a>0,f(x)的对称轴是x=1,且ab=2.
∴f(x)在[1,+∞)上单调递增.
又∵7+|t|≥7,1+t2≥1,
∴由f(7+|t|)>f(1+t2),得7+|t|>1+t2.
∴|t|2-|t|-6<0,解得-3<t<3.
探究创新
7.已知二次函数f(x)=x2+bx+c(b、c∈R),不论α、β为何实数,恒有f(sinα)≥0,f(2+cosβ)≤0.
(1)求证:b+c=-1;
(2)求证:c≥3;
(3)若函数f(sinα)的最大值为8,求b、c的值.
(1)证明:∵|sinα|≤1且f(sinα)≥0恒成立,可得f(1)≥0.
又∵1≤2+cosβ≤3且f(2+cosβ)≤0恒成立,可得f(1)≤0,
∴f(1)=0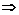 1+b+c=0
1+b+c=0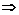 b+c=-1.
b+c=-1.
(2)证明:∵b+c=-1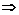 b=-1-c,
b=-1-c,
∴f(x)=x2-(1+c)x+c=(x-1)(x-c).
∴x-c≤0,即c≥x恒成立.∴c≥3.
(3)解:∵f(sinα)=sin2α-(1+c)sinα+c=(sinα-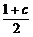 )2+c-(
)2+c-(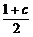 )2,
)2,
∴当sinα=-1时,f(sinα)的最大值为1-b+c.
由1-b+c=8与b-c=-1联立可得b=-4,c=3.
6.(2004年江西九校联考三月)已知函数f(x)=-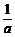 +
+ (x>0).
(x>0).
(1)判断f(x)在(0,+∞)上的单调性,并证明;
(2)解关于x的不等式f(x)>0;
(3)若f(x)+2x≥0在(0,+∞)上恒成立,求a的取值范围.
解:(1)f(x)在(0,+∞)上为减函数,
∵ (x)=-
(x)=- <0,
<0,
∴f(x)在(0,+∞)上为减函数.
(2)由f(x)>0得-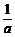 +
+ >0,
>0,
即 <0.
<0.
①当a>0时,不等式解集为{x|0<x<2a}.
②当a<0时,原不等式为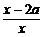 >0.
>0.
解集为{x|x>0}.
(3)若f(x)+2x≥0在(0,+∞)上恒成立,
即-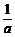 +
+ +2x≥0.∴
+2x≥0.∴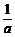 ≤
≤ +2x.
+2x.
∵ +2x≥4,∴
+2x≥4,∴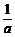 ≤4.
≤4.
解得a<0或a≥ .
.
5.设p=(log2x)2+(t-2)log2x-t+1,若t在区间[-2,2]上变动时,p恒为正值,试求x的取值范围.
解:p=(log2x-1)t+(log2x)2-2log2x+1,∵t∈[-2,2]时p恒为正值,
∴
解得1<log2x<3.∴2<x<8.
培养能力
4.已知定义在(0,+∞)上的函数f(x)满足①x>1时,f(x)<0;(2)f( )=1;(3)对任意的x、y∈(0,+∞),都有f(xy)=f(x)+f(y),求不等式f(x)+f(5-x)≥-2的解集.
)=1;(3)对任意的x、y∈(0,+∞),都有f(xy)=f(x)+f(y),求不等式f(x)+f(5-x)≥-2的解集.
解:需先研究y=f(x)的单调性,任取x1、x2∈(0,+∞)且x1>x2,则 >1.
>1.
f(x1)=f( ·x2)=f(
·x2)=f( )+f(x2),
)+f(x2),
∴f(x1)-f(x2)=f( )<0.
)<0.
∴f(x)在(0,+∞)上为减函数.
又f(1)=f(1)+f(1),则f(1)=0.
又∵f(1)=f(2)+f( )=f(2)+1=0.
)=f(2)+1=0.
∴f(2)=-1.∴f(4)=2f(2)=-2.
∴原不等式等价于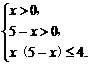
解得{x|0<x≤1或4≤x<5}.
3.在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小,1= .
.
解析:设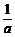 +
+ =1,a、b∈N*,则a=
=1,a、b∈N*,则a=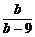 .
.
∴a+b=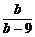 +b+1,b>9时,
+b+1,b>9时,
a+b=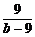 +b-9+10≥16.
+b-9+10≥16.
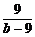 =b-9,即b=12取等号,此时a=4.
=b-9,即b=12取等号,此时a=4.
b<9无解.∴a=4,b=12.
答案:4 12
2.如果对任意实数x,不等式|x+1|≥kx恒成立,则实数k的范围是____________.
解析:画出y1=|x+1|,y2=kx的图象,由图可看出0≤k≤1.
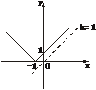
答案:0≤k≤1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com