2.在解答有关直线的问题时，要注意(1)在确定直线的斜率、倾斜角时，首先要注意斜率存在的条件，其次是倾斜角的范围；(2)在利用直线的截距式解题时，要注意防止由于“零截距”而造成丢解的情况；(3)在利用直线的点斜式、斜截式解题时，要注意检验斜率不存在的情况，防止丢解；(4)要灵活运用定比分点公式、中点坐标公式，在解决有关分割问题、对称问题时可以简化运算；(5)掌握对称问题的四种基本类型的解法；(6)在由两直线的位置关系确定有关参数的值或其范围时，要充分利用分类讨论、数形结合、特殊值检验等基本的数学思想方法．

1.要能分辨线段的有向与无向概念上的混淆，有向线段的数量与有向线段长度的混淆，能否分清这两点是学好有向线段的关键．

3.由于一次函数的图象是一条直线，因此有关函数、数列、不等式、复数等代数问题往往借助直线方程进行解决，考查学生的综合能力及创新能力.

在复习本章时要注意如下几点：

2.直线与圆、圆锥曲线的位置关系等综合性试题的难度较大，一般以解答题形式出现(此类问题下一章重点复习).

1.本章在高考中主要考查两类问题：

基本概念题和求在不同条件下的直线方程.基本概念重点考查：(1)与直线方程特征值(主要指斜率、截距)有关的问题；(2)直线的平行和垂直的条件；(3)与距离有关的问题等.此类题大都属于中、低档题，以选择题和填空题形式出现，每年必考.中心对称与轴对称问题虽然在《考试大纲》中没有提及，但也是高考的重点，复习时也应很好地掌握.

2.加强利用均值不等式及其他方法求最值的练习，在求最大(小)值时，有三个问题必须注意：第一，注意不等式成立的充分条件，即x＞0，y＞0(x+y≥2)；第二，注意一定要出现积为定值或和为定值；第三，要注意等号成立的条件，若等号不成立，利用均值不等式x+y≥2不能求出最大(小)值.

拓展题例

[例1] 设f(x)=ax²+bx+c，若f(1)=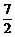，问是否存在a、b、c∈R，使得不等式x²+≤f(x)≤2x²+2x+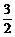对一切实数x都成立，证明你的结论.

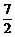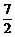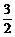
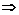解：由f(1)=，得a+b+c=.令x²+=2x²+2x+x=－1.

由f(x)≤2x²+2x+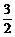推得f(－1)≤，

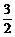由f(x)≥x²+推得f(－1)≥，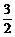

∴f(－1)=.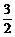

∴a－b+c=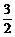.故a+c=且b=1.

∴f(x)=ax²+x+－a.

依题意ax²+x+－a≥x²+对一切x∈R都成立，

∴a≠1且Δ=1－4(a－1)(2－a)≤0.

由a－1＞0得a=.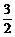

∴f(x)=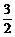x²+x+1.

证明如下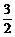：x²+x+1－2x²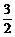－2x－=－x²－x－=－(x+1)²≤0.

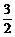∴x²+x+1≤2x²+2x+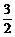对x∈R都成立.

∴存在实数a=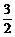，b=1，c=1，使得不等式x²+≤f(x)≤2x²+2x+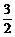对一切x∈R都成立.

[例2] 已知二次函数y=ax²+2bx+c，其中a＞b＞c且a+b+c=0.

(1)求证：此函数的图象与x轴交于相异的两个点.

(2)设函数图象截x轴所得线段的长为l，求证：＜l＜2.

证明：(1)由a+b+c=0得b=－(a+c).

Δ=(2b)²－4ac=4(a+c)²－4ac

=4(a²+ac+c²)=4［(a+)²+c²］＞0.

故此函数图象与x轴交于相异的两点.

(2)∵a+b+c=0且a＞b＞c，

∴a＞0，c＜0.

由a＞b得a＞－(a+c)，

∴＞－2.

由b＞c得－(a+c)＞c，

∴＜－.

∴－2＜＜－.

l=|x₁－x₂|=.

由二次函数的性质知l∈(，2).

1.在解不等式时，要注意函数思想、数形结合思想、分类讨论思想的应用.

4.不等式应用的特点是：(1)问题的背景是人们关心的社会热点问题，如“物价、税收、销售、市场、信息”等，题目往往篇幅较长；(2)建立函数模型常见的有“正(反)比例函数、一次函数、二次函数、指数函数、对数函数、三角函数，以及y=ax+(a＞0，b＞0)、y=ax²+、y=k(a+b)x·(c－ax)(d－bx)”的形式.

3.建立不等式的主要途径有：利用问题的几何意义；利用判别式；利用函数的有界性；利用函数的单调性；利用均值不等式.