
2.(2004年湖南,2)设直线ax+by+c=0的倾斜角为α,且sinα+cosα=0,则a、b满足
A.a+b=1 B.a-b=1 C.a+b=0 D.a-b=0
解析:0°≤α<180°,又sinα+cosα=0,α=135°,∴a-b=0.
答案:D
1.直线x-2y+2k=0与两坐标轴所围成的三角形面积不大于1,那么k的范围是
A.k≥-1
B.k≤1
C.-1≤k≤1且k≠0
D.k≤-1或k≥1
解析:令x=0,得y=k;令y=0,得x=-2k.∴三角形面积S= |xy|=k2.
|xy|=k2.
又S≤1,即k2≤1,
∴-1≤k≤1.
又∵k=0时不合题意,故选C.
答案:C
5.下列四个命题:①经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示;②经过任意两个不同的点P1(x1,y1)、P2(x2,y2)的直线都可以用方程(x2-x1)(x-x1)=(y2-y1)(y-y1)表示;③不经过原点的直线都可以用方程 +
+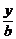 =1表示;④经过定点 A(0,b)的直线都可以用方程y=kx+b表示.其中真命题的个数是
=1表示;④经过定点 A(0,b)的直线都可以用方程y=kx+b表示.其中真命题的个数是
A.0 B.1 C.2 D.3
解析:对命题①④,方程不能表示倾斜角是90°的直线,对命题③,当直线平行于一条坐标轴时,则直线在该坐标轴上截距不存在,故不能用截距式表示直线.只有②正确.
答案:B
●典例剖析
[例1] 已知△ABC的三个顶点是A(3,-4)、B(0,3)、C(-6,0),求它的三条边所在的直线方程.
剖析:一条直线的方程可写成点斜式、斜截式、两点式、截距式和一般式等多种形式.使用时,应根据题目所给的条件恰当选择某种形式,使得解法简便.由顶点B与C的坐标可知点B在y轴上,点C在x轴上,于是BC边所在的直线方程用截距式表示,AB所在的直线方程用斜截式的形式表示,AC所在的直线方程利用两点式或点斜式表示均可,最后为统一形式,均化为直线方程的一般式.
解:如下图,因△ABC的顶点B与C的坐标分别为(0,3)和(-6,0),故B点在y轴上,C点在x轴上,即直线BC在x轴上的截距为-6,在y轴上的截距为3,利用截距式,直线BC的方程为 +
+ =1,
=1,

化为一般式为x-2y+6=0.
由于B点的坐标为(0,3),故直线AB在y轴上的截距为3,利用斜截式,得直线AB的方程为y=kx+3.
又由顶点A(3,-4)在其上,所以-4=3k+3.故k=-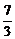 .
.
于是直线AB的方程为y=-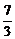 x+3,化为一般式为7x+3y-9=0.
x+3,化为一般式为7x+3y-9=0.
由A(3,-4)、C(-6,0),
得直线AC的斜率kAC= =-
=- .
.
利用点斜式得直线AC的方程为
y-0=- (x+6),
(x+6),
化为一般式为4x+9y+24=0.
也可用两点式,得直线AC的方程为
 =
= ,
,
再化简即可.
评述:本题考查了求直线方程的基本方法.
[例2] 已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),求过两点Q1(a1,b1)、Q2(a2,b2)(a1≠a2)的直线方程.
剖析:利用点斜式或直线与方程的概念进行解答.
解:∵P(2,3)在已知直线上,
|
 2a1+3b1+1=0,
2a1+3b1+1=0,
2a2+3b2+1=0.
∴2(a1-a2)+3(b1-b2)=0,即 =-
=- .
.
∴所求直线方程为y-b1=- (x-a1).
(x-a1).
∴2x+3y-(2a1+3b1)=0,即2x+3y+1=0.
评述:此解法运用了整体代入的思想,方法巧妙.
思考讨论
依“两点确定一直线”,那么你又有新的解法吗?
提示: 由
 2a1+3b1+1=0,
2a1+3b1+1=0,
2a2+3b2+1=0,
知Q1、Q2在直线2x+3y+1=0上.
[例3] 一条直线经过点P(3,2),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍;
(2)与x、y轴的正半轴交于A、B两点,且△AOB的面积最小(O为坐标原点).
剖析:(2)将面积看作截距a、b的函数,求函数的最小值即可.
解:(1)设所求直线倾斜角为θ,已知直线的倾斜角为α,则θ=2α,且tanα= ,tanθ=tan2α=
,tanθ=tan2α= ,
,
从而方程为8x-15y+6=0.
(2)设直线方程为 +
+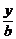 =1,a>0,b>0,代入P(3,2),得
=1,a>0,b>0,代入P(3,2),得 +
+ =1≥2
=1≥2 ,得ab≥24,
,得ab≥24,
从而S△AOB= ab≥12,
ab≥12,
此时 =
= ,∴k=-
,∴k=-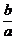 =-
=- .
.
∴方程为2x+3y-12=0.
评述:此题(2)也可以转化成关于a或b的一元函数后再求其最小值.
深化拓展
若求|PA|·|PB|及|OA|+|OB|的最小值,又该怎么解呢?
提示: 可类似第(2)问求解.
●闯关训练
夯实基础
4.直线y=1与直线y= x+3的夹角为___________.
x+3的夹角为___________.
解法一:l1:y=1与l2:y= x+3的斜率分别为k1=0,k2=
x+3的斜率分别为k1=0,k2= .由两直线的夹角公式得 tanα=|
.由两直线的夹角公式得 tanα=|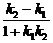 |=
|= ,所以两直线的夹角为60°.
,所以两直线的夹角为60°.
解法二:l1与l2表示的图象为(如下图所示)y=1与x轴平行,y= x+3与x轴倾斜角为60°,所以y=1与y=
x+3与x轴倾斜角为60°,所以y=1与y= x+3的夹角为60°.
x+3的夹角为60°.

答案:60°
3.直线xcosα+ y+2=0的倾斜角范围是
y+2=0的倾斜角范围是
A.[ ,
, )∪(
)∪( ,
, ]
]
B.[0, ]∪[
]∪[ ,π)
,π)
C.[0, ]
]
D.[ ,
, ]
]
解析:设直线的倾斜角为θ,
则tanθ=- cosα.又-1≤cosα≤1,
cosα.又-1≤cosα≤1,
∴- ≤tanθ≤
≤tanθ≤ .∴θ∈[0,
.∴θ∈[0, ]∪[
]∪[ ,π).
,π).
答案:B
2.过两点(-1,1)和(3,9)的直线在x轴上的截距是
A.- B.-
B.- C.
C. D.2
D.2
解析:求出过(-1,1)、(3,9)两点的直线方程,令y=0即得.
答案:A
1.直线xtan +y=0的倾斜角是
+y=0的倾斜角是
A.- B.
B. C.
C. D.
D.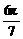
解析:k=-tan =tan(π-
=tan(π- )=tan
)=tan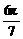 且
且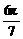 ∈[0,π).
∈[0,π).
答案:D
2.直线方程的五种形式
(1)斜截式:y=kx+b.
(2)点斜式:y-y0=k(x-x0).
(3)两点式: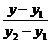 =
= .
.
(4)截距式: +
+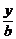 =1.
=1.
(5)一般式:Ax+By+C=0.
●点击双基
1.直线的倾斜角、斜率及直线的方向向量
(1)直线的倾斜角
在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α,那么α就叫做直线的倾斜角.
当直线和x轴平行或重合时,我们规定直线的倾斜角为0°.
可见,直线倾斜角的取值范围是0°≤α<180°.
(2)直线的斜率
倾斜角α不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用k表示,即k=tanα(α≠90°).
倾斜角是90°的直线没有斜率;倾斜角不是90°的直线都有斜率,其取值范围是(-∞,+∞).
(3)直线的方向向量
设F1(x1,y1)、F2(x2,y2)是直线上不同的两点,则向量 =(x2-x1,y2-y1)称为直线的方向向量.向量
=(x2-x1,y2-y1)称为直线的方向向量.向量
 =(1,
=(1,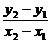 )=(1,k)也是该直线的方向向量,k是直线的斜率.
)=(1,k)也是该直线的方向向量,k是直线的斜率.
(4)求直线斜率的方法
①定义法:已知直线的倾斜角为α,且α≠90°,则斜率k=tanα.
②公式法:已知直线过两点P1(x1,y1)、P2(x2,y2),且x1≠x2,则斜率k=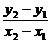 .
.
③方向向量法:若a=(m,n)为直线的方向向量,则直线的斜率k= .
.
平面直角坐标系内,每一条直线都有倾斜角,但不是每一条直线都有斜率.
斜率的图象如下图.
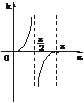
对于直线上任意两点P1(x1,y1)、P2(x2,y2),当x1=x2时,直线斜率k不存在,倾斜角α=90°;当x1≠x2时,直线斜率存在,是一实数,并且k≥0时,α=arctank,k<0时,α=π+arctank.
7.1 直线的方程
●知识梳理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com