
3.如何建立平面坐标系内满足一定条件的直线的方程是本节的主要问题;通用的解决方法是待定系数法;根据所知条件选择恰当的直线方程的形式是解题的关键;克服各类方程局限性的手段是分类讨论;开阔思路分析问题的措施是数形结合.
拓展题例
[例1] 在直线方程y=kx+b中,当x∈[-3,4]时,y∈[-8,13],求此直线方程.
 解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
-3k+b=-8,
4k+b=13,
|
 k=3,
k=3,
b=1,
∴直线方程为y=3x+1.
 当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
-3k+b=13,
4k+b=-8,
|
 k=-3,
k=-3,
b=4.
∴所求的直线方程为y=-3x+4.
[例2] 已知两点A(-1,2)、B(m,3).
(1)求直线AB的斜率k与倾斜角α;
(2)求直线AB的方程;
(3)已知实数m∈[- -1,
-1, -1],求直线AB的倾斜角α的取值范围.
-1],求直线AB的倾斜角α的取值范围.
解:(1)当m=-1时,直线AB的斜率不存在,倾斜角α= .
.
当m≠-1时,k=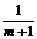 ,
,
当m>-1时,α=arctan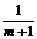 ,
,
当m<-1时,α=π+arctan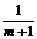 .
.
(2)当m=-1时,AB:x=-1,
当m≠1时,AB:y-2=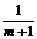 (x+1).
(x+1).
(3)1°当m=-1时,α= ;
;
2°当m≠-1时,
∵k=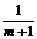 ∈(-∞,-
∈(-∞,- ]∪[
]∪[ ,+∞),
,+∞),
∴α∈[ ,
, )∪(
)∪( ,
, ].
].
故综合1°、2°得,直线AB的倾斜角α∈[ ,
, ].
].
2.直线方程的点斜式、两点式、斜截式、截距式等都是直线方程的特殊形式,其中点斜式是最基本的,其他形式的方程皆可由它推导.直线方程的特殊形式都具有明显的几何意义,但又都有一些特定的限制条件,因此应用时要注意它们各自适用的范围,以避免漏解.
1.注意斜率和倾斜角的区别,让学生了解斜率的图象.
9.某市现有自市中心O通往正西和东北方向的两条主要公路,为了解决交通拥挤问题,市政府决定修一条环城路,分别在通往正西和东北方向的公路上选取A、B两点,使环城公路在A、B间为线段,要求AB环城路段与中心O的距离为10 km,且使A、B间的距离|AB|最小,请你确定A、B两点的最佳位置(不要求作近似计算).
解:以O为原点,正东方向为x轴的正半轴,正北方向为y轴的正半轴,建立如下图所示的坐标系.

设A(-a,0)、B(b,b)(其中a>0,b>0),
则AB的方程为 =
=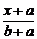 ,
,
即bx-(a+b)y+ab=0.
∵10= ,
,
∴a2b2=100(a2+2b2+2ab)
≥100(2 +2ab)
+2ab)
=200(1+ )ab.
)ab.
∵ab>0,
∴ab≥200( +1).
+1).
当且仅当“a2=2b2”时等号成立,
而|AB|=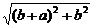 =
= ,
,
∴|AB|≥20( +1).
+1).
|
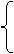 a2=2b2,
a2=2b2,
ab=10 ,
,
|
|
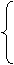 a=10
a=10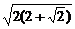 ,
,
b=10
此时|OA|=a=10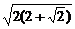 ,
,
|OB|=10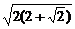 ,
,
∴A、B两点的最佳位置是离市中心O均为10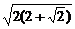 km处.
km处.
●思悟小结
直线的倾斜角、斜率及直线在坐标轴上的截距是刻画直线位置状态的基本量,应正确理解;直线方程有五种形式,其中点斜式要熟练掌握,这五种形式的方程表示的直线各有适用范围,解题时应注意不要丢解;含参数的直线方程问题用数形结合法常常简捷些.
●教师下载中心
教学点睛
8.(文)已知点P(1,-1),直线l的方程为 x-2y+1=0.求经过点P,且倾斜角为直线l的倾斜角一半的直线方程.
x-2y+1=0.求经过点P,且倾斜角为直线l的倾斜角一半的直线方程.
解:设直线l的倾斜角为α,则所求直线的倾斜角为 ,由已知直线l的斜率为tanα=
,由已知直线l的斜率为tanα= 及公式tanα=
及公式tanα= ,得
,得
tan2 +2
+2 ·tan
·tan -1=0.
-1=0.
解得tan =
= -
- 或tan
或tan =-
=- -
- .
.
由于tanα= ,而0<
,而0< <1,故0<α<
<1,故0<α<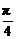 ,0<
,0< <
<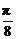 .因此tan
.因此tan >0.
>0.
于是所求直线的斜率为k=tan =
= -
- .
.
故所求的直线方程为y-(-1)=( -
- )(x-1),
)(x-1),
即( -
- )x-y-(
)x-y-( -
- +1)=0.
+1)=0.
(理)设直线l的方程是2x+By-1=0,倾斜角为α.
(1)试将α表示为B的函数;
(2)若 <α<
<α< ,试求B的取值范围;
,试求B的取值范围;
(3)若B∈(-∞,-2)∪(1,+∞),求α的取值范围.
解:(1)若B=0,则直线l的方程是2x-1=0,∴α= ;
;
若B≠0,则方程即为y=-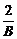 x+
x+ ,
,
∴当B<0时,-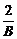 >0,α=arctan(
>0,α=arctan(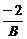 ),
),
而当B>0时,-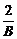 <0,α=π+arctan(-
<0,α=π+arctan(-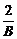 ),
),
 -arctan
-arctan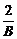 (B<0),
(B<0),
|
 (B=0),
(B=0),
π-arctan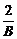 (B>0).
(B>0).
(2)若α= ,则B=0,
,则B=0,
若α≠ ,则tanα<-
,则tanα<- 或tanα>
或tanα> ,
,
即-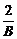 <-
<- (B>0)或-
(B>0)或-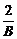 =>
=> (B<0),
(B<0),
∴-2 <B<0或0<B<
<B<0或0<B<
 .
.
综上,知-2 <B<
<B<
 .
.
(3)若B<-2,则-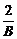 <1,
<1,
∴0<tanα<1,0<α<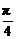 ;
;
若B>1,则-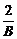 >-2,
>-2,
∴0>tanα>-2,π-arctan2<α<π.
综上,知π-arctan2<α<π或0<α<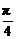 .
.
探究创新
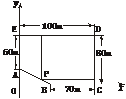
7.某房地产公司要在荒地ABCDE(如下图)上划出一块长方形地面(不改变方位)建造一幢八层的公寓楼,问如何设计才能使公寓占地面积最大?并求出最大面积.(精确到1 m2)

解:如下图,在线段AB上任取一点P,
分别向CD、DE作垂线划得一块长方形土地,建立如下图所示的直角坐标系,则AB的方程为 +
+ =1.设P(x,20-
=1.设P(x,20- x),则长方形面积S=(100-x)[80-(20-
x),则长方形面积S=(100-x)[80-(20- x)]
(0≤x≤30).
x)]
(0≤x≤30).
化简得S=- x2+
x2+ x+6000(0≤x≤30).
x+6000(0≤x≤30).
配方,易得x=5,y= 时,S最大,其最大值为6017 m2.
时,S最大,其最大值为6017 m2.
6.在△ABC中,已知点A(5,-2)、B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
解:(1)设点C(x,y),由题意得 =0,
=0,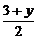 =0,得x=-5,y=-3.故所求点C的坐标是(-5,-3).
=0,得x=-5,y=-3.故所求点C的坐标是(-5,-3).
(2)点M的坐标是(0,-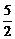 ),点N的坐标是(1,0),直线MN的方程是
),点N的坐标是(1,0),直线MN的方程是 =
=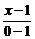 ,
,
即5x-2y-5=0.
培养能力
5.已知直线l的斜率为6,且被两坐标轴所截得的线段长为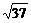 ,求直线l的方程.
,求直线l的方程.
解法一:设所求直线l的方程为y=kx+b.
∵k=6,∴方程为y=6x+b.
令x=0,∴y=b,与y轴的交点为(0,b);
令y=0,∴x=-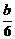 ,与x轴的交点为(-
,与x轴的交点为(-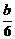 ,0).
,0).
根据勾股定理得(-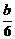 )2+b2=37,
)2+b2=37,
∴b=±6.因此直线l的方程为y=6x±6.
解法二:设所求直线为 +
+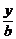 =1,则与x轴、y轴的交点分别为(a,0)、(0,b).
=1,则与x轴、y轴的交点分别为(a,0)、(0,b).
由勾股定理知a2+b2=37.
又k=-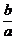 =6,
=6,
|
|
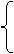 a2+b2=37,
a2+b2=37,
-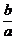 =6.
=6.
|

 a=1, a=-1,
a=1, a=-1,
b=-6 b=6.
因此所求直线l的方程为x+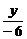 =1或-x+
=1或-x+ =1,即6x-y±6=0.
=1,即6x-y±6=0.
4.(2005年北京东城区目标检测)已知直线l1:x-2y+3=0,那么直线l1的方向向量a1为____________(注:只需写出一个正确答案即可);l2过点(1,1),并且l2的方向向量a2与a1满足a1·a2=0,则l2的方程为____________.
解析:由方向向量定义即得a1为(2,1)或(1, ).
).
a1·a2=0,即a1⊥a2.
也就是l1⊥l2,即k1·k2=-1.
再由点斜式可得l2的方程为2x+y-3=0.
答案:(2,1)或(1, ) 2x+y-3=0
) 2x+y-3=0
3.(2004年春季北京)直线x- y+a=0(a为实常数)的倾斜角的大小是____________.
y+a=0(a为实常数)的倾斜角的大小是____________.
解析:k= ,即tanα=
,即tanα= .
.
∴α=30°.
答案:30°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com