
2.在运用一条直线到另一条直线的角的公式时要注意无斜率的情况及两条直线垂直的情况.
1.要认清直线平行、垂直的充要条件,应特别注意对x、y的系数中一个为零的情况的讨论.
9.已知三条直线l1:2x-y+a=0(a>0),直线l2:-4x+2y+1=0和直线l3:x+y-1=0,且l1与l2的距离是
 .
.
(1)求a的值;
(2)求l3到l1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的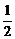 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是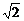 ∶
∶ ?若能,求P点坐标;若不能,请说明理由.
?若能,求P点坐标;若不能,请说明理由.
解:(1)l2即2x-y-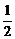 =0,
=0,
∴l1与l2的距离d= =
= .
.
∴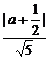 =
= .∴|a+
.∴|a+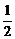 |=
|=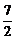 .
.
∵a>0,∴a=3.
(2)由(1),l1即2x-y+3=0,∴k1=2.而l3的斜率k3=-1,
∴tanθ=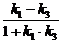 =
= =-3.
=-3.
∵0≤θ<π,∴θ=π-arctan3.
(3)设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线l′:2x-y+C=0上,
且 =
=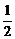
 ,即C=
,即C= 或C=
或C= ,
,
∴2x0-y0+ =0或2x0-y0+
=0或2x0-y0+ =0;
=0;
若P点满足条件③,由点到直线的距离公式,
有 =
=
 ,
,
即|2x0-y0+3|=|x0+y0-1|,
∴x0-2y0+4=0或3x0+2=0.
由P在第一象限,∴3x0+2=0不可能.
联立方程2x0-y0+ =0和x0-2y0+4=0,
=0和x0-2y0+4=0,
|
|
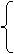 x0=-3,
x0=-3,
y0=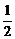 ,
,
|
 2x0-y0+
2x0-y0+ =0,
=0,
x0-2y0+4=0,
|
 x0=
x0= ,
,
y0= .
.
∴P( ,
, )即为同时满足三个条件的点.
)即为同时满足三个条件的点.
●思悟小结
8.(理)已知过点A(1,1)且斜率为-m(m>0)的直线l与x轴、y轴分别交于P、Q,过P、Q作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ面积的最小值.
解:设l的方程为y-1=-m(x-1),
则P(1+ ,0),Q(0,1+m).
,0),Q(0,1+m).
从而可得直线PR和QS的方程分别为
x-2y- =0和x-2y+2(m+1)=0.
=0和x-2y+2(m+1)=0.
又PR∥QS,
∴|RS|=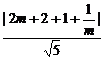
=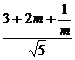 .又|PR|=
.又|PR|= ,
,
|QS|= ,
,
四边形PRSQ为梯形,
S四边形PRSQ=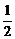 [
[ +
+ ]·
]·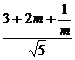
= (m+
(m+ +
+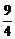 )2-
)2- ≥
≥ (2+
(2+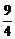 )2-
)2- =3.6.
=3.6.
∴四边形PRSQ的面积的最小值为3.6.
(文)在△ABC中,已知BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在直线的方程为y=0.若点B的坐标为(1,2),求点C的坐标.
解:点A为y=0与x-2y+1=0两直线的交点,
∴点A的坐标为(-1,0).
∴kAB= =1.
=1.
又∵∠A的平分线所在直线的方程是y=0,
∴k AC=-1.
∴直线AC的方程是y=-x-1.
而BC与x-2y+1=0垂直,∴kBC=-2.
∴直线BC的方程是y-2=-2(x-1).
|
 y=-x-1,
y=-x-1,
y=-2x+4,
解得C(5,-6).
探究创新
7.在平面直角坐标系中,在y轴的正半轴(原点除外)上给定两点A(0,a)、B(0,b)(a>b>0).试在x轴的正半轴(原点除外)上求点C,使∠ACB取得最大值,并求出这个最大值.
解:由题意作下图,设C(x,0),其中x>0.
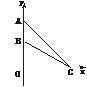
又A(0,a),B(0,b)(a>b>0),
则kAC=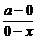 =-
=- ,
,
kBC= =-
=-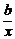 .
.
∴tan∠ACB= =
= =
= ≤
≤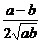 .此时x=
.此时x= 时取等号.故所求点C(
时取等号.故所求点C( ,0),最大值为arctan
,0),最大值为arctan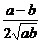 .
.
6.光线从A(-3,4)点射出,到x轴上的B点后,被x轴反射到y轴上的C点,又被y轴反射,这时反射线恰好过点D(-1,6),求BC所在直线的方程.
解法一:如下图所示,依题意,B点在原点O左侧,设坐标为(a,0),由入射角等于反射角得∠1=∠2,∠3=∠4,

∴kAB=-kBC.
又kAB=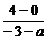 =-
=- (a≠-3),
(a≠-3),
∴kBC= .∴BC的方程为y-0=
.∴BC的方程为y-0= (x-a),即4x-(3+a)y-4a=0.
(x-a),即4x-(3+a)y-4a=0.
令x=0,解得C点坐标为(0, ),
),
则kDC= =-
=- .
.
∵∠3=∠4,∴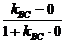 =
= .
.
∴ =
= .
.
解得a=-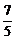 ,
,
代入BC方程得5x-2y+7=0.
解法二:点A关于x轴的对称点为A′(-3,-4),点D关于y轴的对称点为D′(1,6),
由入射角等于反射角及对顶角相等可知A′、D′都在直线BC上,
∴BC的方程为5x-2y+7=0.
5.已知△ABC的两条高线所在直线的方程为2x-3y+1=0和x+y=0,顶点A(1,2),求:
(1)BC边所在直线的方程;
(2)△ABC的面积.
解:(1)A点不在两条高线上,从而AB、AC边所在直线方程为3x+2y-7=0,x-y+1=0.
∴C(-2,-1)、B(7,-7).
∴边BC所在直线方程是2x+3y+7=0.
(2)∵|BC|= ,点A到边BC的高为h=
,点A到边BC的高为h= ,从而△ABC的面积是
,从而△ABC的面积是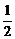 ×3
×3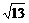 ×
× =
= .
.
培养能力
4.求过点P(5,-2),且与直线x-y+5=0相交成45°角的直线l的方程.
解:(1)若直线l的斜率存在,设为k,由题意,tan45°=|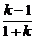 |,得k=0,所求l的直线方程为y=-2.
|,得k=0,所求l的直线方程为y=-2.
(2)若直线l的斜率不存在,则直线l的方程为x=5,且与直线x-y+5=0相交成45°角.
综合(1)(2),直线l的方程为x=5或y=-2.
3.△ABC中,a、b、c是内角A、B、C的对边,且lgsinA,lgsinB,lgsinC成等差数列,则下列两条直线l1:(sin2A)x+(sinA)y-a=0,l2:(sin2B)x+(sinC)y-c=0的位置关系是____________.
解析:由已知2lgsinB=lgsinA+lgsinC,
得lg(sinB)2=lg(sinA·sinC).
∴sin2B=sinA·sinC.
设l1:a1x+b1y+c1=0,l2:a2x+b2y+c2=0.
∵ =
= =
= =
=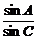 ,
,
 =
=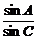 ,
,
 =
=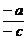 =
= =
=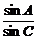 ,
,
∴ =
= =
= ,l1与l2重合.
,l1与l2重合.
答案:重合
2.若直线y=|x|与y=kx+1有两个交点,则k的取值范围是____________.
解析:y=|x|是第一、二象限角的平分线,直线y=kx+1是过定点(0,1)的直线系方程.
由图象易知-1<k<1.
答案:-1<k<1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com