
2.(2004年浙江,理4)曲线y2=4x关于直线x=2对称的曲线方程是
A.y2=8-4x B.y2=4x-8
C.y2=16-4x D.y2=4x-16
解析:设曲线y2=4x关于直线x=2对称的曲线为C,在曲线C上任取一点P(x,y),则P(x,y)关于直线x=2的对称点为Q(4-x,y).因为Q(4-x,y)在曲线y2=4x上,
所以y2=4(4-x),即y2=16-4x.
答案:C
1.已知点M(a,b)与N关于x轴对称,点P与点N关于y轴对称,点Q与点P关于直线x+y=0对称,则点Q的坐标为
A.(a,b) B.(b,a)
C.(-a,-b) D.(-b,-a)
解析:N(a,-b),P(-a,-b),则Q(b,a).
答案:B
4.两点关于点对称、两点关于直线对称的常见结论:
(1)点(x,y)关于x轴的对称点为(x,-y);
(2)点(x,y)关于y轴的对称点为(-x,y);
(3)点(x,y)关于原点的对称点为(-x,-y);
(4)点(x,y)关于直线x-y=0的对称点为(y,x);
(5)点(x,y)关于直线x+y=0的对称点为(-y,-x).
●点击双基
3.曲线关于点、曲线关于直线的中心或轴对称问题,一般是转化为点的中心对称或轴对称(这里既可选特殊点,也可选任意点实施转化).一般结论如下:
(1)曲线f(x,y)=0关于已知点A(a,b)的对称曲线的方程是f(2a-x,2b-y)=0.
(2)曲线f(x,y)=0关于直线y=kx+b的对称曲线的求法:
设曲线f(x,y)=0上任意一点为P(x0,y0),P点关于直线y=kx+b的对称点为P′(y,x),则由(2)知,P与P′的坐标满足
|
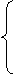
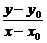 ·k=-1,
·k=-1,
 =k·
=k·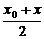 +b,
+b,
代入已知曲线f(x,y)=0,应有f(x0,y0)=0.利用坐标代换法就可求出曲线f(x,y)=0关于直线y=kx+b的对称曲线方程.
2.点关于直线成轴对称问题
由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”.利用“垂直”“平分”这两个条件建立方程组,就可求出对顶点的坐标.一般情形如下:
设点P(x0,y0)关于直线y=kx+b的对称点为P′(x′,y′),则有
|
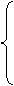
 ·k=-1,
·k=-1,
 =k·
=k· +b,
+b,
特殊地,点P(x0,y0)关于直线x=a的对称点为P′(2a-x0,y0);点P(x0,y0)关于直线y=b的对称点为P′(x0,2b-y0).
1.点关于点成中心对称的对称中心恰是这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题.
设P(x0,y0),对称中心为A(a,b),则P关于A的对称点为P′(2a-x0,2b-y0).
7.3 对称问题
●知识梳理
2.在判断两直线的位置关系时,也可利用直线方程的一般式,由系数间的关系直接作出结论,设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
(1)l1∥l2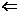
 =
=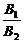 ≠
≠
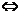
 A1B2=A2B1,
A1B2=A2B1,
A1C2≠A2C1.
(2)l1与l2相交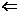
 ≠
≠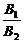
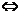 A1B2≠A2B1.
A1B2≠A2B1.
(3)l1与l2重合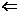
 =
=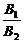 =
=
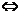
 A1B2=A2B1,
A1B2=A2B1,
A1C2=A2C1.
(4)l1⊥l2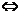 A1A2+B1B2=0.
A1A2+B1B2=0.
拓展题例
[例1] 当0<a<2时,直线l1:ax-2y=2a-4,直线l2:2x+a2y=2a2+4与坐标轴围成一个四边形,求使该四边形面积最小时a的值.
解:直线l1交y轴于A(0,2-a),直线l2交x轴于C(a2+2,0),l1与l2交于点B(2,2).
则四边形AOCB的面积为S=S△AOB+S△OCB=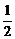 ·(2-a)·2+
·(2-a)·2+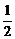 (a2+2)·2=a2-a+4=(a-
(a2+2)·2=a2-a+4=(a-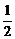 )2+
)2+ ,
,
当a=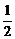 时,S最小.
时,S最小.
因此使四边形面积最小时a的值为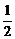 .
.
[例2] 已知n条直线l1:x-y+C1=0,C1=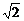 ,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
(1)求Cn;
(2)求x-y+Cn=0与x轴、y轴围成的图形的面积;
(3)求x-y+Cn-1=0与x-y+Cn=0及x轴、y轴围成图形的面积.
解:(1)原点O到l1的距离为1,原点O到l2的距离为1+2,……原点O到ln的距离dn为1+2+…+n= .
.
∵Cn=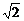 dn,
dn,
∴Cn= .
.
(2)设直线ln:x-y+Cn=0交x轴于M,交y轴于N,则△OMN面积
S△O MN=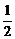 |OM|·|ON|=
|OM|·|ON|=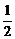 Cn2=
Cn2= .
.
(3)所围成的图形是等腰梯形,由(2)知Sn= ,则有Sn-1=
,则有Sn-1=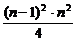 .
.
∴Sn-Sn-1= -
-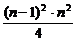 =n3.
=n3.
∴所求面积为n3.
1.两条直线的位置关系的有关内容是本章学习的重点,在整个解析几何的学习中占有重要地位.这部分内容是用代数方法研究几何图形的具体应用.
3.点到直线的距离公式是一个基本公式,它涉及绝对值、直线垂直、最小值等内容.
●教师下载中心
教学点睛
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com