
7.若抛物线y=2x2上的两点A(x1,y1)、B(x2,y2)关于直线y=x+m对称且x1x2=-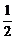 ,求m的值.
,求m的值.
解:设直线AB的方程为y=-x+b,代入y=2x2得2x2+x-b=0,
∴x1+x2=-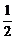 ,x1x2=
,x1x2=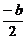 =-
=-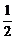 .
.
∴b=1,即AB的方程为y=-x+1.
设AB的中点为M(x0,y0),则
x0=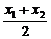 =-
=-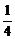 ,代入y0=-x0+1,
,代入y0=-x0+1,
得y0=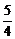 .又M(-
.又M(-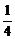 ,
,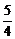 )在y=x+m上,
)在y=x+m上,
∴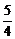 =-
=-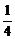 +m.∴m=
+m.∴m=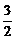 .
.
6.求函数y=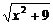 +
+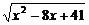 的最小值.
的最小值.
解:因为y=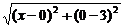 +
+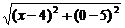 ,
,
所以函数y是x轴上的点P(x,0)与两定点A(0,3)、B(4,3)距离之和.
y的最小值就是|PA|+|PB|的最小值.
由平面几何知识可知,若A关于x轴的对称点为A ′(0,-3),
则|PA|+|PB|的最小值等于|A′B|,
即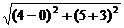 =4
=4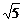 .
.
所以ymin=4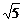 .
.
5.已知△ABC的一个顶点A(-1,-4),∠B、∠C的平分线所在直线的方程分别为l1:y+1=0,l2:x+y+1=0,求边BC所在直线的方程.
解:设点A(-1,-4)关于直线y+1=0的对称点为A′(x1,y1),则x1=-1,y1=2×(-1)-(-4)=2,即A′(-1,2).
在直线BC上,再设点A(-1,-4)关于l2:x+y+1=0的对称点为A″(x2,y2),则有
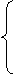
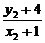 ×(-1)=-1,
×(-1)=-1,
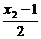 +
+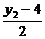 +1=0.
+1=0.
|
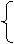 x2=3,
x2=3,
y2=0,
即A″(3,0)也在直线BC上,由直线方程的两点式得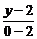 =
=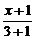 ,即x+2y-3=0为边BC所在直线的方程.
,即x+2y-3=0为边BC所在直线的方程.
培养能力
4.直线2x-y-4=0上有一点P,它与两定点A(4,-1)、B(3,4)的距离之差最大,则P点的坐标是____________.
解析:易知A(4,-1)、B(3,4)在直线l:2x-y-4=0的两侧.作A关于直线l的对称点A1(0,1),当A1、B、P共线时距离之差最大.
答案:(5,6)
3.两直线y=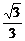 x和x=1关于直线l对称,直线l的方程是____________.
x和x=1关于直线l对称,直线l的方程是____________.
解析:l上的点为到两直线y=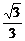 x与x=1距离相等的点的集合,即
x与x=1距离相等的点的集合,即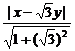 =|x-1|,化简得x+
=|x-1|,化简得x+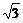 y-2=0或3x-
y-2=0或3x-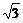 y-2=0.
y-2=0.
答案:x+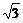 y-2=0或3x-
y-2=0或3x-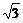 y-2=0
y-2=0
2.与直线x+2y-1=0关于点(1,-1)对称的直线方程为
A.2x-y-5=0 B.x+2y-3=0
C.x+2y+3=0 D.2x-y-1=0
解析:将x+2y-1=0中的x、y分别代以2-x,-2-y,得(2-x)+2(-2-y)-1=0,即x+2y+3=0.故选C.
答案:C
1.(2004年全国卷Ⅱ,4)已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆C的方程为
A.(x+1)2+y2=1 B.x2+y2=1
C.x2+(y+1)2=1 D.x2+(y-1)2=1
解析:由M(x,y)关于y=-x的对称点为(-y,-x),
即得x2+(y+1)2=1.
答案:C
5.设直线x+4y-5=0的倾斜角为θ,则它关于直线y-3=0对称的直线的倾斜角是____________.
解析:数形结合.
答案:π-θ
●典例剖析
[例1] 求直线a:2x+y-4=0关于直线l:3x+4y-1=0对称的直线b的方程.
剖析:由平面几何知识可知若直线a、b关于直线l对称,它们具有下列几何性质:(1)若a、b相交,则l是a、b交角的平分线;(2)若点A在直线a上,那么A关于直线l的对称点B一定在直线b上,这时AB⊥l,并且AB的中点D在l上;(3)a以l为轴旋转180°,一定与b重合.使用这些性质,可以找出直线b的方程.解此题的方法很多,总的来说有两类:一类是找出确定直线方程的两个条件,选择适当的直线方程的形式,求出直线方程;另一类是直接由轨迹求方程.
|
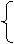
|
3x+4y-1=0,
方法一:设直线b的斜率为k,又知直线a的斜率为-2,直线l的斜率为-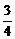 .
.
则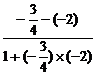 =
=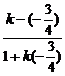 .
.
解得k=-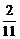 .
.
代入点斜式得直线b的方程为
y-(-2)=-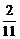 (x-3),
(x-3),
即2x+11y+16=0.
方法二:在直线a:2x+y-4=0上找一点A(2,0),设点A关于直线l的对称点B的坐标为(x0,y0),
|
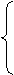 3×
3×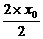 +4×
+4×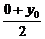 -1=0,
-1=0,
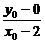 =
=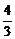 ,
,
解得B(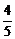 ,-
,-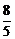 ).
).
由两点式得直线b的方程为
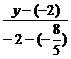 =
=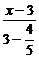 ,
,
即2x+11y+16=0.
方法三:设直线b上的动点P(x,y)关于l:3x+4y-1=0的对称点Q(x0,y0),则有
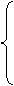 3×
3×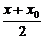 +4×
+4×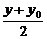 -1=0,
-1=0,
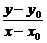 =
=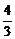 .
.
解得x0=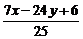 ,y0=
,y0=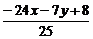 .
.
Q(x0,y0)在直线a:2x+y-4=0上,
则2×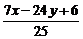 +
+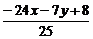 -4=0,
-4=0,
化简得2x+11y+16=0是所求直线b的方程.
方法四:设直线b上的动点P(x,y),直线a上的点Q(x0,4-2x0),且P、Q两点关于直线l:3x+4y-1=0对称,则有
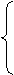
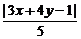 =
=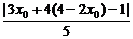 ,
,
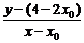 =
=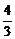 .
.
消去x0,得2x+11y+16=0或2x+y-4=0(舍).
评述:本题体现了求直线方程的两种不同的途径,方法一与方法二,除了点E外,分别找出确定直线位置的另一个条件:斜率或另一个点,然后用点斜式或两点式求出方程,方法三与方法四是利用直线上动点的几何性质,直接由轨迹求方程,在使用这种方法时,要注意区分动点坐标及参数,本题综合性较强,只有对坐标法有较深刻的理解,同时有较强的数形结合能力才能较好地完成此题.
[例2] 光线从点A(-3,4)发出,经过x轴反射,再经过y轴反射,光线经过点 B(-2,6),求射入y轴后的反射线的方程.
剖析:由物理中光学知识知,入射线和反射线关于法线对称.
解:∵A(-3,4)关于x轴的对称点A1(-3,-4)在经x轴反射的光线上,
同样A1(-3,-4)关于y轴的对称点A2(3,-4)在经过射入y轴的反射线上,
∴k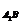 =
= =-2.
=-2.
故所求直线方程为y-6=-2(x+2),
即2x+y-2=0.
评述:注意知识间的相互联系及学科间的相互渗透.
[例3] 已知点M(3,5),在直线l:x-2y+2=0和y轴上各找一点P和Q,使△MPQ的周长最小.
剖析:如下图,作点M关于直线l的对称点M1,再作点M关于y轴的对称点M2,连结MM1、MM2,连线MM1、MM2与l及y轴交于P与Q两点,由轴对称及平面几何知识,可知这样得到的△MPQ的周长最小.
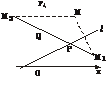
解:由点M(3,5)及直线l,可求得点M关于l的对称点M1(5,1).同样容易求得点M关于y轴的对称点M2(-3,5).
据M1及M2两点可得到直线M1M2的方程为x+2y-7=0.
|
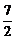 ).
).
|
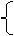 x+2y-7=0,
x+2y-7=0,
x-2y+2=0,
故点P(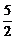 ,
,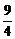 )、Q(0,
)、Q(0,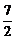 )即为所求.
)即为所求.
评述:恰当地利用平面几何的知识对解题能起到事半功倍的效果.
深化拓展
恰当地利用平面几何的知识解题.
不妨再试试这个小题:已知点A(1,3)、B(5,2),在x轴上找一点P,使得|PA|+|PB|最小,则最小值为____________,P点的坐标为____________.
答案: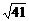 (
(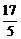 ,0)
,0)
●闯关训练
夯实基础
4.点A(4,5)关于直线l的对称点为B(-2,7),则l的方程为____________.
解析:对称轴是以两对称点为端点的线段的中垂线.
答案:3x-y+3=0
3.已知直线l1:x+my+5=0和直线l2:x+ny+p=0,则l1、l2关于y轴对称的充要条件是
A.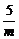 =
=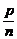
B.p=-5
C.m=-n且p=-5
D.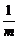 =-
=-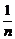 且p=-5
且p=-5
解析:直线l1关于y轴对称的直线方程为(-x)+my+5=0,即x-my-5=0,与l2比较,
∴m=-n且p=-5.反之亦验证成立.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com