
6.某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
解:设每盒盒饭需要面食x(百克),米食y(百克),

所需费用为S=0.5x+0.4y,且x、y满足
 6x+3y≥8,
6x+3y≥8,
4x+7y≥10,
x≥0,
y≥0,
由图可知,直线y=-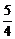 x+
x+ S过A(
S过A( ,
,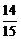 )时,纵截距
)时,纵截距 S最小,即S最小.
S最小,即S最小.
故每盒盒饭为面食 百克,米食
百克,米食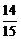 百克时既科学又费用最少.
百克时既科学又费用最少.
培养能力
5.画出以A(3,-1)、B(-1,1)、C(1,3)为顶点的△ABC的区域(包括各边),写出该区域所表示的二元一次不等式组,并求以该区域为可行域的目标函数z=3x-2y的最大值和最小值.
分析:本例含三个问题:①画指定区域;②写所画区域的代数表达式--不等式组; ③求以所写不等式组为约束条件的给定目标函数的最值.
解:如图,连结点A、B、C,则直线AB、BC、CA所围成的区域为所求△ABC区域.

直线AB的方程为x+2y-1=0,BC及CA的直线方程分别为x-y+2=0,2x+y-5=0.
在△ABC内取一点P(1,1),分别代入x+2y-1,x-y+2,2x+y-5得x+2y-1>0,x-y+2>0,2x+y-5<0.
因此所求区域的不等式组为
 x+2y-1≥0,
x+2y-1≥0,
x-y+2≥0,
2x+y-5≤0.
作平行于直线3x-2y=0的直线系3x-2y=t(t为参数),即平移直线y= x,观察图形可知:当直线y=
x,观察图形可知:当直线y= x-
x- t过A(3,-1)时,纵截距-
t过A(3,-1)时,纵截距- t最小.此时t最大,tmax=3×3-2× (-1)=11;
t最小.此时t最大,tmax=3×3-2× (-1)=11;
当直线y= x-
x- t经过点B(-1,1)时,纵截距-
t经过点B(-1,1)时,纵截距- t最大,此时t有最小值为tmin= 3×(-1)-2×1=-5.
t最大,此时t有最小值为tmin= 3×(-1)-2×1=-5.
 因此,函数z=3x-2y在约束条件
因此,函数z=3x-2y在约束条件
|
x-y+2≥0,
2x+y-5≤0
3.(2004年全国卷Ⅱ,14)设x、y满足约束条件
 x≥0,
x≥0,
x≥y,
2x-y≤1,则z=3x+2y的最大值是____________.
解析:如图,当x=y=1时,zmax=5.

答案:5
|
 x-4y+3≤0,
x-4y+3≤0,
|
x≥1,
_________.
解析:作出可行域,如图.当把z看作常数时,它表示直线y=zx的斜率,因此,当直线y=zx过点A时,z最大;当直线y=zx过点B时,z最小.
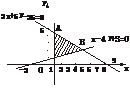
|
 x=1,
x=1,
3x+5y-25=0,得A(1, ).
).
|
|
 x-4y+3=0,
x-4y+3=0,
3x+5y-25=0,
∴zmax= =
= ,zmin=
,zmin= .
.
答案:

2.(x+2y+1)(x-y+4)≤0表示的平面区域为
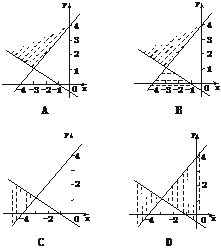
解析:可转化为

|
 x+2y+1≥0, x+2y+1≤0,
x+2y+1≥0, x+2y+1≤0,
x-y+4≤0 x-y+4≥0.
答案:B
1.(x-1)2+(y-1)2=1是|x-1|+|y-1|≤1的__________条件.
A.充分而不必要 B.必要而不充分
C.充分且必要 D.既不充分也不必要
解析:数形结合.
答案:B
5.不等式组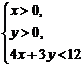 表示的平面区域内的整点(横坐标和纵坐标都是整数的点)共有____________个.
表示的平面区域内的整点(横坐标和纵坐标都是整数的点)共有____________个.
解析:(1,1),(1,2),(2,1),共3个.
答案:3
●典例剖析
[例1] 求不等式|x-1|+|y-1|≤2表示的平面区域的面积.
剖析:依据条件画出所表达的区域,再根据区域的特点求其面积.
解:|x-1|+|y-1|≤2可化为



|
|

|
y≥1, y≤1, y≥1, y≤1,
x+y ≤4 x-y ≤2 y-x ≤2 x+y≥0.
其平面区域如图.
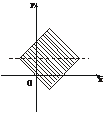
∴面积S= ×4×4=8.
×4×4=8.
评述:画平面区域时作图要尽量准确,要注意边界.
深化拓展
若再求:①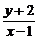 ;②
;② 的值域,你会做吗?
的值域,你会做吗?
答案: ①(-∞,- ]∪[
]∪[ ,+∞);②[1,5].
,+∞);②[1,5].
[例2] 某人上午7时,乘摩托艇以匀速v n mile/h(4≤v≤20)从A港出发到距50 n mile的B港去,然后乘汽车以匀速w km/h(30≤w≤100)自B港向距300 km的C市驶去.应该在同一天下午4至9点到达C市.设乘汽车、摩托艇去所需要的时间分别是x h、y h.
(1)作图表示满足上述条件的x、y范围;
(2)如果已知所需的经费
p=100+3×(5-x)+2×(8-y)(元),
那么v、w分别是多少时走得最经济?此时需花费多少元?
剖析:由p=100+3×(5-x)+2×(8-y)可知影响花费的是3x+2y的取值范围.
解:(1)依题意得v=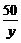 ,w=
,w= ,4≤v≤20,30≤w≤100.
,4≤v≤20,30≤w≤100.
∴3≤x≤10, ≤y≤
≤y≤ . ①
. ①
由于乘汽车、摩托艇所需的时间和x+y应在9至14个小时之间,即9≤x+y≤14.②
因此,满足①②的点(x,y)的存在范围是图中阴影部分(包括边界).

(2)∵p=100+3·(5-x)+2·(8-y),
∴3x+2y=131-p.
设131-p=k,那么当k最大时,p最小.在通过图中的阴影部分区域(包括边界)且斜率为- 的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当x=10,y=4时,p最小.
的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当x=10,y=4时,p最小.
此时,v=12.5,w=30,p的最小值为93元.
评述:线性规划问题首先要根据实际问题列出表达约束条件的不等式.然后分析要求量的几何意义.
[例3] 某矿山车队有4辆载重量为10 t的甲型卡车和7辆载重量为6 t的乙型卡车,有9名驾驶员.此车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次.甲型卡车每辆每天的成本费为252元,乙型卡车每辆每天的成本费为160元.问每天派出甲型车与乙型车各多少辆,车队所花成本费最低?
剖析:弄清题意,明确与运输成本有关的变量的各型车的辆数,找出它们的约束条件,列出目标函数,用图解法求其整数最优解.
解:设每天派出甲型车x辆、乙型车y辆,车队所花成本费为z元,那么
 x+y≤9,
x+y≤9,
10×6x+6×8x≥360,
0≤x≤4,
0≤y≤7.
z=252x+160y,
其中x、y∈N.
作出不等式组所表示的平面区域,即可行域,如图.

作出直线l0:252x+160y=0,把直线l向右上方平移,使其经过可行域上的整点,且使在y轴上的截距最小.观察图形,可见当直线252x+160y=t经过点(2,5)时,满足上述要求.
此时,z=252x+160y取得最小值,即x=2,y=5时,zmin=252×2+160×5=1304.
答:每天派出甲型车2辆,乙型车5辆,车队所用成本费最低.
评述:用图解法解线性规划题时,求整数最优解是个难点,对作图精度要求较高,平行直线系f(x,y)=t的斜率要画准,可行域内的整点要找准,最好使用“网点法”先作出可行域中的各整点.
●闯关训练
夯实基础
4.点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是________________.
解析:(-2,t)在2x-3y+6=0的上方,则2×(-2)-3t+6<0,解得t> .
.
答案:t>
2.(2005年海淀区期末练习题)设动点坐标(x,y)满足
|
 (x-y+1)(x+y-4)≥0,
(x-y+1)(x+y-4)≥0,
x≥3,
A.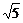 B.
B. C.
C.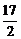 D.10
D.10
解析:数形结合可知当x=3,y=1时,x2+y2的最小值为10.
答案:D
|
|
 2x-y+1≥0,
2x-y+1≥0,
x-2y-1≤0,
x+y≤1
A.正三角形及其内部
B.等腰三角形及其内部
C.在第一象限内的一个无界区域
D.不包含第一象限内的点的一个有界区域
解析:将(0,0)代入不等式组适合C,不对;将( ,
, )代入不等式组适合D,不对;又知2x-y+1=0与x-2y-1=0关于y=x对称且所夹顶角α满足
)代入不等式组适合D,不对;又知2x-y+1=0与x-2y-1=0关于y=x对称且所夹顶角α满足
tanα=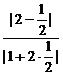 =
= .
.
∴α≠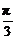 .
.
答案:B
1.下列命题中正确的是
A.点(0,0)在区域x+y≥0内
B.点(0,0)在区域x+y+1<0内
C.点(1,0)在区域y>2x内
D.点(0,1)在区域x-y+1>0内
解析:将(0,0)代入x+y≥0,成立.
答案:A
2.线性规划
求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
满足线性约束条件的解(x,y)叫做可行解,由所有可行解组成的集合叫做可行域(类似函数的定义域);使目标函数取得最大值或最小值的可行解叫做最优解.生产实际中有许多问题都可以归结为线性规划问题.
线性规划问题一般用图解法,其步骤如下:
(1)根据题意,设出变量x、y;
(2)找出线性约束条件;
(3)确定线性目标函数z=f(x,y);
(4)画出可行域(即各约束条件所示区域的公共区域);
(5)利用线性目标函数作平行直线系f(x,y)=t(t为参数);
(6)观察图形,找到直线f(x,y)=t在可行域上使t取得欲求最值的位置,以确定最优解,给出答案.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com