
4.(2005年北京海淀区期末练习)将圆x2+y2=1按向量a平移得到圆(x+1)2+(y-2)2=1,则a的坐标为____________.
解析:由向量平移公式即得a=(-1,2).
答案:(-1,2)
3.已知圆的方程为(x-a)2+(y-b)2=r2(r>0),下列结论错误的是
A.当a2+b2=r2时,圆必过原点
B.当a=r时,圆与y轴相切
C.当b=r时,圆与x轴相切
D.当b<r时,圆与x轴相交
解析:已知圆的圆心坐标为(a,b),半径为r,当b<r时,圆心到x轴的距离为|b|,只有当|b|<r时,才有圆与x轴相交,而b<r不能保证|b|<r,故D是错误的.故选D.
答案:D
2.点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是
A.|a|<1
B.a<
C.|a|< D.|a|<
D.|a|<
解析:点P在圆(x-1)2+y2=1内部
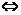 (5a+1-1)2+(12a)2<1
(5a+1-1)2+(12a)2<1
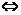 |a|<
|a|< .
.
答案:D
1.方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)表示圆方程,则t的取值范围是
A.-1<t<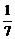 B.-1<t<
B.-1<t<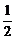
C.-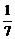 <t<1
D.1<t<2
<t<1
D.1<t<2
解析:由D2+E2-4F>0,得7t2-6t-1<0,
即-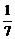 <t<1.
<t<1.
答案:C
2.二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件
若上述二元二次方程表示圆,则有A=C≠0,B=0,这仅是二元二次方程表示圆的必要条件,不充分.
在A=C≠0,B=0时,二元二次方程化为x2+y2+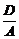 x+
x+ y+
y+ =0,
=0,
仅当(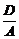 )2+(
)2+( )2-4·
)2-4· >0,即D2+E2-4AF>0时表示圆.
>0,即D2+E2-4AF>0时表示圆.
故Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是:①A=C≠0,②B=0,③D2+E2-4AF>0.
●点击双基
1.圆的方程
(1)圆的标准方程
圆心为(a,b),半径为r的圆的标准方程为(x-a)2+(y-b)2=r2.
说明:方程中有三个参量a、b、r,因此三个独立条件可以确定一个圆.
(2)圆的一般方程
二次方程x2+y2+Dx+Ey+F=0.(*)
将(*)式配方得
(x+ )2+(y+
)2+(y+ )2=
)2= .
.
当D2+E2-4F>0时,方程(*)表示圆心(- ,-
,- ),半径r=
),半径r=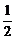
 的圆,把方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)叫做圆的一般方程.
的圆,把方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)叫做圆的一般方程.
说明:(1)圆的一般方程体现了圆方程的代数特点:
a.x2、y2项系数相等且不为零.
b.没有xy项.
(2)当D2+E2-4F=0时,方程(*)表示点(- ,-
,- ),当D2+E2-4F<0时,方程(*)不表示任何图形.
),当D2+E2-4F<0时,方程(*)不表示任何图形.
(3)据条件列出关于D、E、F的三元一次方程组,可确定圆的一般方程.
(3)圆的参数方程
①圆心在O(0,0),半径为r的圆的参数方程为
|
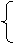 x=rcosθ,
x=rcosθ,
y=rsinθ
②圆心在O1(a,b),半径为r的圆的参数方程为
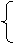
|
y=b+rsinθ
说明:在①中消去θ得x2+y2=r2,在②中消去θ得(x-a)2+(y-b)2=r2,把这两个方程相对于它们各自的参数方程又叫做普通方程.
7.5 圆的方程
●知识梳理
9.实系数方程f(x)=x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,求:
(1)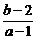 的值域;
的值域;
(2)(a-1)2+(b-2)2的值域;
(3)a+b-3的值域.

|
 f(0)>0
f(0)>0
f(1)<0
f(2)>0
 b>0,
b>0,
a+b+1<0,
a+b+2>0.
如图所示. A(-3,1)、B(-2,0)、C(-1,0).

又由所要求的量的几何意义知,值域分别为(1)( ,1);(2)(8,17);(3)(-5,-4).
,1);(2)(8,17);(3)(-5,-4).
●思悟小结
简单的线性规划在实际生产生活中应用非常广泛,主要解决的问题是:在资源的限制下,如何使用资源来完成最多的生产任务;或是给定一项任务,如何合理安排和规划,能以最少的资源来完成.如常见的任务安排问题、配料问题、下料问题、布局问题、库存问题,通常解法是将实际问题转化为数学模型,归结为线性规划,使用图解法解决.
图解法解决线性规划问题时,根据约束条件画出可行域是关键的一步.一般地,可行域可以是封闭的多边形,也可以是一侧开放的非封闭平面区域.第二是画好线性目标函数对应的平行直线系,特别是其斜率与可行域边界直线斜率的大小关系要判断准确.通常最优解在可行域的顶点(即边界线的交点)处取得,但最优整数解不一定是顶点坐标的近似值.它应是目标函数所对应的直线平移进入可行域最先或最后经过的那一整点的坐标.
●教师下载中心
教学点睛
线性规划是新增添的教学内容,应予以足够重视.
线性规划问题中的可行域,实际上是二元一次不等式(组)表示的平面区域,是解决线性规划问题的基础,因为在直线Ax+By+C=0同一侧的所有点(x,y)实数Ax+By+C的符号相同,所以只需在此直线的某一侧任取一点(x0,y0)(若原点不在直线上,则取原点(0,0)最简便),把它的坐标代入Ax+By+C=0,由其值的符号即可判断二元一次不等式Ax+By+C>0(或<0)表示直线的哪一侧.这是教材介绍的方法.
在求线性目标函数z=ax+by的最大值或最小值时,设ax+by=t,则此直线往右(或左)平移时,t值随之增大(或减小),要会在可行域中确定最优解.
解线性规划应用题步骤:(1)设出决策变量,找出线性约束条件和线性目标函数; (2)利用图象在线性约束条件下找出决策变量,使线性目标函数达到最大(或最小).
拓展题例
[例1] 已知f(x)=px2-q且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的范围.
解:∵-4≤f(1)≤-1,-1≤f(2)≤5,
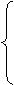 p-q≤-1,
p-q≤-1,
|
4p-q≤5,
4p-q≥-1.
求z=9p-q的最值.

|
 p=0,
p=0,
q=1,
zmin=-1,
|
 p=3,
p=3,
q=7,
∴-1≤f(3)≤20.
[例2] 某汽车公司有两家装配厂,生产甲、乙两种不同型号的汽车,若A厂每小时可完成1辆甲型车和2辆乙型车;B厂每小时可完成3辆甲型车和1辆乙型车.今欲制造40辆甲型车和20辆乙型车,问这两家工厂各工作几小时,才能使所费的总工作时数最少?
解:设A厂工作x h,B厂工作y h,总工作时数为t h,则t=x+y,且x+3y≥40,2x+y≥20,x≥0,y≥0,可行解区域如图.而符合问题的解为此区域内的格子点(纵、横坐标都是整数的点称为格子点),于是问题变为要在此可行解区域内,找出格子点(x,y),使t=x+y的值为最小.

由图知当直线l:y=-x+t过Q点时,纵、横截距t最小,但由于符合题意的解必须是格子点,我们还必须看Q点是否是格子点.
|
 x+3y=40,
x+3y=40,
2x+y=20,
得Q(4,12)为格子点.
故A厂工作4 h,B厂工作12 h,可使所费的总工作时数最少.
8.某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
|
资 金 |
单位产品所需资金(百元) |
月资金供应量(百元) |
|
|
空调机 |
洗衣机 |
||
|
成 本 |
30 |
20 |
300 |
|
劳动力(工资) |
5 |
10 |
110 |
|
单位利润 |
6 |
8 |
|
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?
解:设空调机、洗衣机的月供应量分别是x、y台,总利润是P,则P=6x+8y,由题意有

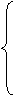 30x+20y≤300,
30x+20y≤300,
5x+10y≤110,
x≥0,
y≥0,
x、y均为整数.
由图知直线y=- x+
x+ P过M(4,9)时,纵截距最大.这时P也取最大值Pmax=6×4+8×9=96(百元).
P过M(4,9)时,纵截距最大.这时P也取最大值Pmax=6×4+8×9=96(百元).
故当月供应量为空调机4台,洗衣机9台时,可获得最大利润9600元.
探究创新
7.配制A、B两种药剂,需要甲、乙两种原料,已知配一剂A种药需甲料3 mg,乙料5 mg;配一剂B种药需甲料5 mg,乙料4 mg.今有甲料20 mg,乙料25 mg,若A、B两种药至少各配一剂,问共有多少种配制方法?
解:设A、B两种药分别配x、y剂(x、y∈N),则
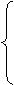 x≥1,
x≥1,
y≥1,
3x+5y≤20,
5x+4y≤25.
上述不等式组的解集是以直线x=1,y=1,3x+5y=20及5x+4y=25为边界所围成的区域,这个区域内的整点为(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)、(3,2)、(4,1).所以,在至少各配一剂的情况下,共有8种不同的配制方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com