
9.(2005年黄冈市调研考试题)如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:
若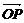 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
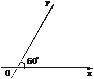
(1)若P点斜坐标为(2,-2),求P到O的距离|PO|;
(2)求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
解:(1)∵P点斜坐标为(2,-2),
∴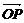 =2e1-2e2.
=2e1-2e2.
∴|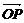 |2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
|2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
∴|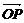 |=2,即|OP|=2.
|=2,即|OP|=2.
(2)设圆上动点M的斜坐标为(x,y),则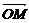 =xe1+ye2.
=xe1+ye2.
∴(xe1+ye2)2=1.
∴x2+y2+2xye1·e2=1.
∴x2+y2+xy=1.
故所求方程为x2+y2+xy=1.
●思悟小结
8.(文)求过两点A(1,4)、B(3,2),且圆心在直线y=0上的圆的标准方程.并判断点M1(2,3),M2(2,4)与圆的位置关系.
解:根据圆的标准方程,只要求得圆心坐标和圆的半径即可.
因为圆过A、B两点,所以圆心在线段AB的垂直平分线上.由kAB= =-1,
=-1,
AB的中点为(2,3),
故AB的垂直平分线的方程为y-3=x-2,
即x-y+1=0.
又圆心在直线y=0上,
因此圆心坐标是方程组
|
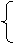 x-y+1=0,
x-y+1=0,
y=0
半径r=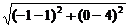 =
=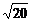 ,
,
所以得所求圆的标准方程为(x+1)2+y2=20.
因为M1到圆心C(-1,0)的距离为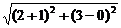 =
= ,|M1C|<r,所以M1在圆C内;而点M2到圆心C的距离|M2C|=
,|M1C|<r,所以M1在圆C内;而点M2到圆心C的距离|M2C|=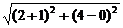 =
=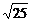 >
>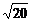 ,所以M2在圆C外.
,所以M2在圆C外.
(理)已知动圆M:x2+y2-2mx-2ny+m2-1=0与圆N:x2+y2+2x+2y-2=0交于A、B两点,且这两点平分圆N的圆周.
(1)求动圆M的圆心的轨迹方程;
(2)求半径最小时圆M的方程.
解:(1)如图所示(坐标系省略了),圆心N(-1,-1)为弦AB的中点,在Rt△AMN中,
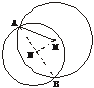
|AM|2=|AN|2+|MN|2,
∴(m+1)2=-2(n+2).(*)
故动圆圆心M的轨迹方程为(x+1)2=-2(y+2).
(2)由(*)式,知(m+1)2=-2(n+2)≥0,
于是有n≤-2.
而圆M半径r=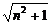 ≥
≥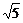 ,
,
∴当r=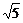 时,n=-2,m=-1,所求圆的方程为(x+1)2+(y+2)2=5.
时,n=-2,m=-1,所求圆的方程为(x+1)2+(y+2)2=5.
探究创新
7.已知实数x、y满足方程x2+y2-4x+1=0.求
(1)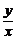 的最大值和最小值;
的最大值和最小值;
(2)y-x的最小值;
(3)x2+y2的最大值和最小值.
解:(1)如图,方程x2+y2-4x+1=0表示以点(2,0)为圆心,以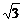 为半径的圆.
为半径的圆.
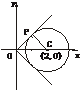
设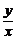 =k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由
=k,即y=kx,由圆心(2,0)到y=kx的距离为半径时直线与圆相切,斜率取得最大、最小值.由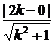 =
=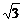 ,
,
解得k2=3.
所以kmax=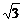 ,kmin=-
,kmin=-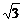 .
.
(也可由平面几何知识,有OC=2,OP=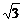 ,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
,∠POC=60°,直线OP的倾斜角为60°,直线OP′的倾斜角为120°解之)
(2)设y-x=b,则y=x+b,仅当直线y=x+b与圆切于第四象限时,纵轴截距b取最小值.由点到直线的距离公式,得
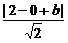 =
=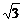 ,即b=-2±
,即b=-2±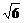 ,
,
故(y-x)min=-2-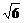 .
.
(3)x2+y2是圆上点与原点距离之平方,故连结OC,与圆交于B点,并延长交圆于C′,则(x2+y2)max=|OC′|=2+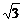 ,
,
(x2+y2)min=|OB|=2-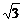 .
.
6.已知实数x、y满足x2+y2+2x-2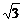 y=0,求x+y的最小值.
y=0,求x+y的最小值.
解:原方程为(x+1)2+(y-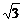 )2=4表示一个圆的方程,可设其参数方程为
)2=4表示一个圆的方程,可设其参数方程为
|
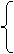 x=-1+2cosθ,
x=-1+2cosθ,
y=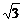 +2sinθ
+2sinθ
2 sin(θ+
sin(θ+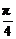 ),当θ=
),当θ=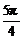 ,即x=-1-
,即x=-1- ,y=
,y=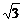 -
- 时,x+y的最小值为
时,x+y的最小值为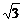 -1-2
-1-2 .
.
培养能力
5.(2005年启东市调研题)设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足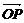 ·
·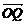 =0.
=0.
(1)求m的值;
(2)求直线PQ的方程.
解:(1)曲线方程为(x+1)2+(y-3)2=9表示圆心为(-1,3),半径为3的圆.
∵点P、Q在圆上且关于直线x+my+4=0对称,
∴圆心(-1,3)在直线上.代入得m=-1.
(2)∵直线PQ与直线y=x+4垂直,
∴设P(x1,y1)、Q(x2,y2),PQ方程为y=-x+b.
将直线y=-x+b代入圆方程,得2x2+2(4-b)x+b2-6b+1=0.
Δ=4(4-b)2-4×2×(b2-6b+1)>0,得2-3 <b<2+3
<b<2+3 .
.
由韦达定理得x1+x2=-(4-b),x1·x2=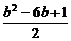 .
.
y1·y2=b2-b(x1+x2)+x1·x2=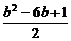 +4b.
+4b.
∵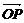 ·
·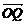 =0,∴x1x2+y1y2=0,
=0,∴x1x2+y1y2=0,
即b2-6b+1+4b=0.
解得b=1∈(2-3 ,2+3
,2+3 ).
).
∴所求的直线方程为y=-x+1.
4.(2004年全国卷Ⅲ,16)设P为圆x2+y2=1上的动点,则点P到直线3x-4y-10=0的 距离的最小值为____________.
解析:圆心(0,0)到直线3x-4y-10=0的距离d= =2.
=2.
再由d-r=2-1=1,知最小距离为1.
答案:1
3.(2005年黄冈市调研题)圆x2+y2+x-6y+3=0上两点P、Q关于直线kx-y+4=0对称,则k=____________.
解析:圆心(-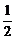 ,3)在直线上,代入kx-y+4=0,得k=2.
,3)在直线上,代入kx-y+4=0,得k=2.
答案:2
2.(2004年全国Ⅱ,8)在坐标平面内,与点A(1,2)距离为1,且与点B(3,1)距离为2的直线共有
A.1条 B.2条 C.3条 D.4条
解析:分别以A、B为圆心,以1、2为半径作圆,两圆的公切线有两条,即为所求.
答案:B
1.方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)表示的曲线关于x+y=0成轴对称图形,则
A.D+E=0B. B.D+F=0
C.E+F=0 D. D+E+F=0
解析:曲线关于x+y=0成轴对称图形,即圆心在x+y=0上.
答案:A
5.已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为____________.
解析:Rt△OMC中,|MP|=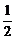 |BC|(直角三角形斜边上的中线是斜边的一半).
|BC|(直角三角形斜边上的中线是斜边的一半).

故所求轨迹方程为x2+y2-x-2y-2=0.
答案:x2+y2-x-2y-2=0
●典例剖析
[例1] (2003年春季北京)设A(-c,0)、B(c,0)(c>0)为两定点,动点P到A点的距离与到B点的距离的比为定值a(a>0),求P点的轨迹.
剖析:给曲线建立方程是解析几何的两个主要问题之一,其基本方法就是把几何条件代数化;主要问题之二是根据方程研究曲线的形状、性质,即用代数的方法研究几何问题.
解:设动点P的坐标为(x,y),由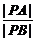 =a(a>0)得
=a(a>0)得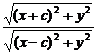 =a,化简,得
=a,化简,得
(1-a2)x2+2c(1+a2)x+c2(1-a2)+(1-a2)y2=0.
当a=1时,方程化为x=0.
当a≠1时,方程化为(x-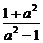 c)2+y2=(
c)2+y2=(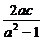 )2.
)2.
所以当a=1时,点P的轨迹为y轴;
当a≠1时,点P的轨迹是以点(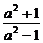 c,0)为圆心,|
c,0)为圆心,|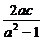 |为半径的圆.
|为半径的圆.
评述:本题主要考查直线、圆、曲线和方程等基本知识,考查运用解析几何的方法解决问题的能力,对代数式的运算化简能力有较高要求.同时也考查了分类讨论这一数学思想.
[例2] 一圆与y轴相切,圆心在直线x-3y=0上,且直线y=x截圆所得弦长为2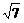 ,求此圆的方程.
,求此圆的方程.
剖析: 利用圆的性质:半弦、半径和弦心距构成的直角三角形.
解:因圆与y轴相切,且圆心在直线x-3y=0上,故设圆方程为(x-3b)2+(y-b)2=9b2.
又因为直线y=x截圆得弦长为2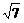 ,
,
则有(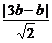 )2+(
)2+(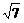 )2=9b2,
)2=9b2,
解得b=±1.故所求圆方程为
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.
评述:在解决求圆的方程这类问题时,应当注意以下几点:(1)确定圆方程首先明确是标准方程还是一般方程;(2)根据几何关系(如本例的相切、弦长等)建立方程求得a、b、r或D、E、F;(3)待定系数法的应用,解答中要尽量减少未知量的个数.
[例3] 已知⊙O的半径为3,直线l与⊙O相切,一动圆与l相切,并与⊙O相交的公共弦恰为⊙O的直径,求动圆圆心的轨迹方程.
剖析:问题中的几何性质十分突出,切线、直径、垂直、圆心,如何利用这些几何性质呢?
解:取过O点且与l平行的直线为x轴,过O点且垂直于l的直线为y轴,建立直角坐标系.
设动圆圆心为M(x,y),
⊙O与⊙M的公共弦为AB,⊙M与l切于点C,则|MA|=|MC|.
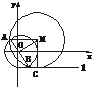
∵AB为⊙O的直径,
∴MO垂直平分AB于O.
由勾股定理得|MA|2=|MO|2+|AO|2=x2+y2+9,而|MC|=|y+3|,
∴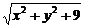 =|y+3|.
=|y+3|.
化简得x2=6y,这就是动圆圆心的轨迹方程.
评述:求轨迹的步骤是“建系,设点,找关系式,除瑕点”.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com