
1.直线和圆位置关系的判定方法一是方程的观点,即把圆的方程和直线的方程联立成方程组,利用判别式Δ来讨论位置关系.
①Δ>0,直线和圆相交.
②Δ=0,直线和圆相切.
③Δ<0,直线和圆相离.
方法二是几何的观点,即把圆心到直线的距离d和半径R的大小加以比较.
①d<R,直线和圆相交.
②d=R,直线和圆相切.
③d>R,直线和圆相离.
7.6 直线与圆的位置关系
●知识梳理
直线和圆
5.数形结合、分类讨论、函数与方程的思想在解决圆的有关问题时经常运用,应熟练掌握.
拓展题例
[例1] 圆x2+y2=1内有一定点A(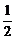 ,0),圆上有两点P、Q,若∠PAQ=90°,求过点P和Q的两条切线的交点M的轨迹方程.
,0),圆上有两点P、Q,若∠PAQ=90°,求过点P和Q的两条切线的交点M的轨迹方程.
分析:先求出PQ中点E的轨迹方程为x2+y2-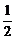 x-
x- =0.
=0.
再求切点弦PQ所在直线的方程.
解:设P(x1,y1),Q(x2,y2),则过P、Q的切线方程分别是
x1x+y1y=1,x2x+y2y=1.
又M(m,n)在这两条切线上,有mx1+ny1=1,mx2+ny2=1,
∵P、Q两点的坐标满足方程mx+ny=1,又两点确定唯一一条直线,
∴PQ所在直线的方程是mx+ny=1.
又∵E为直线OM与PQ之交点,解方程组
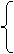 mx+ny=1
mx+ny=1
y=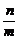 x
x
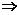 x=
x= ,y=
,y= .
.
将( ,
, )代入中点E的轨迹方程得x2+y2+
)代入中点E的轨迹方程得x2+y2+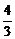 x-
x-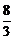 =0.
=0.
这就是要求的过P、Q两点的切线交点M的轨迹方程.
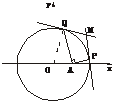
[例2] 如图,过原点的动直线交圆x2+(y-1)2=1于点Q,在直线OQ上取点P,使P到直线y=2的距离等于|PQ|,求动直线绕原点转一周时P点的轨迹方程.

解:设P(x,y),圆O1:x2+(y-1)2=1与直线y=2切于点A,连结AQ,易知|AQ|=|AR|=|x|,
又|PQ|=|PR|=2-y,
∴在Rt△OQA中,|OA|2=|AQ|2+|OQ|2,
即22=|x|2+[ -(2-y)]2,
-(2-y)]2,
化简整理得x2(x2+y2-4)=0,
∴x=0或x2+y2=4为所求的轨迹方程.
4.在解决与圆有关的问题时,要充分利用圆的特殊几何性质,这样会使问题简单化.
3.在一般方程中,当D2+E2-4F=0时,方程表示一个点(- ,-
,- ),当D2+E2-4F<0时,无轨迹.
),当D2+E2-4F<0时,无轨迹.
2.如果问题中给出了圆心两坐标之间的关系或圆心的特殊位置时,一般用标准方程.如果给出圆上的三个点的坐标,一般用一般方程.
1.在二元二次方程中x2和y2的系数相等并且没有x、y项只是表示圆的必要条件而不是充分条件.
3.解析几何中与圆有关的问题,应充分运用圆的几何性质帮助解题.
●教师下载中心
教学点睛
2.求圆的方程的一般步骤:
(1)选用圆的方程两种形式中的一种(若知圆上三个点的坐标,通常选用一般方程;若给出圆心的特殊位置或圆心与两坐标间的关系,通常选用标准方程);
(2)根据所给条件,列出关于D、E、F或a、b、r的方程组;
(3)解方程组,求出D、E、F或a、b、r的值,并把它们代入所设的方程中,得到所求圆的方程.
1.不论圆的标准方程还是一般方程,都有三个字母(a、b、r或D、E、F)的值需要确定,因此需要三个独立的条件.利用待定系数法得到关于a、b、r(或D、E、F)的三个方程组成的方程组,解之得到待定字母系数的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com