
3.(2005年春季北京,11)若圆x2+y2+mx-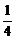 =0与直线y=-1相切,且其圆心在y轴的左侧,则m的值为____________.
=0与直线y=-1相切,且其圆心在y轴的左侧,则m的值为____________.
解析:圆方程配方得(x+ )2+y2=
)2+y2= ,圆心为(-
,圆心为(- ,0).
,0).
由条件知- <0,即m>0.
<0,即m>0.
又圆与直线y=-1相切,则0-(-1)=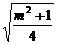 ,即m2=3,∴m=
,即m2=3,∴m= .
.
答案:
2.(2003年春季北京)已知直线ax+by+c=0(abc≠0)与圆x2+y2=1相切,则三条边长分别为|a|、|b|、|c|的三角形
A.是锐角三角形 B.是直角三角形
C.是钝角三角形 D.不存在
解析:由题意得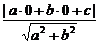 =1,即c2=a2+b2,∴由|a|、|b|、|c|构成的三角形为直角三角形.
=1,即c2=a2+b2,∴由|a|、|b|、|c|构成的三角形为直角三角形.
答案:B
1.若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y=2的距离等于1,则半径r的范围是
A.(4,6) B.[4,6) C.(4,6] D.[4,6]
解析:数形结合法解.
答案:A
5.若直线y=x+k与曲线x= 恰有一个公共点,则k的取值范围是___________.
恰有一个公共点,则k的取值范围是___________.
解析:利用数形结合.
答案:-1<k≤1或k=-
●典例剖析
[例1] 已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
剖析:由于OP⊥OQ,所以kOP·kOQ=-1,问题可解.
解:将x=3-2y代入方程x2+y2+x-6y+m=0,得5y2-20y+12+m=0.
设P(x1,y1)、Q(x2,y2),则y1、y2满足条件
y1+y2=4,y1y2= .
.
∵OP⊥OQ,∴x1x2+y1y2=0.
而x1=3-2y1,x2=3-2y2,
∴x1x2=9-6(y1+y2)+4y1y2.
∴m=3,此时Δ>0,圆心坐标为(-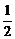 ,3),半径r=
,3),半径r= .
.
评述:在解答中,我们采用了对直线与圆的交点“设而不求”的解法技巧,但必须注意这样的交点是否存在,这可由判别式大于零帮助考虑.
[例2] 求经过两圆(x+3)2+y2=13和x2+(y+3)2=37的交点,且圆心在直线x-y-4=0上的圆的方程.
剖析:根据已知,可通过解方程组
|
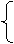 (x+3)2+y2=13,
(x+3)2+y2=13,
x2+(y+3)2=37
由圆心在直线x-y-4=0上,三个独立条件,用待定系数法求出圆的方程;
也可根据已知,设所求圆的方程为(x+3)2+y2-13+λ[x2+(y+3)2-37]=0,再由圆心在直线x-y-4=0上,定出参数λ,得圆方程.
解:因为所求的圆经过两圆(x+3)2+y2=13和x2+(y+3)2=37的交点,
所以设所求圆的方程为(x+3)2+y2-13+λ[x2+(y+3)2-37]=0.
展开、配方、整理,得(x+ )2+(y+
)2+(y+ )2=
)2= +
+ .
.
圆心为(- ,-
,- ),代入方程x-y-4=0,得λ=-7.
),代入方程x-y-4=0,得λ=-7.
故所求圆的方程为(x+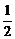 )2+(y+
)2+(y+ )2=
)2=  .
.
评述:圆C1:x2+y2+D1x+E1y+F1=0,圆C2:x2+y2+D2x+E2y+F2=0,若圆C1、C2相交,那么过两圆公共点的圆系方程为(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0(λ∈R且λ≠-1).它表示除圆C2以外的所有经过两圆C1、C2公共点的圆.
特别提示
在过两圆公共点的图象方程中,若λ=-1,可得两圆公共弦所在的直线方程.
[例3] 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明:不论m取什么实数,直线l与圆恒交于两点;
(2)求直线被圆C截得的弦长最小时l的方程.
剖析:直线过定点,而该定点在圆内,此题便可解得.
(1)证明:l的方程(x+y-4)+m(2x+y-7)=0.
|
|
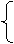 2x+y-7=0, x=3,
2x+y-7=0, x=3,
x+y-4=0, y=1,
即l恒过定点A(3,1).
∵圆心C(1,2),|AC|=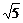 <5(半径),
<5(半径),
∴点A在圆C内,从而直线l恒与圆C相交于两点.
(2)解:弦长最小时,l⊥AC,由kAC=-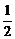 ,
,
∴l的方程为2x-y-5=0.
评述:若定点A在圆外,要使直线与圆相交则需要什么条件呢?
思考讨论
求直线过定点,你还有别的办法吗?
●闯关训练
夯实基础
4.(2004年上海,理8)圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0,-4)、B(0,-2),则圆C的方程为____________.
解析:∵圆C与y轴交于A(0,-4),B(0,-2),
∴由垂径定理得圆心在y=-3这条直线上.
又已知圆心在直线2x-y-7=0上,
|
|
 y=-3,
y=-3,
2x-y-7=0.
∴圆心为(2,-3),
半径r=|AC|= =
=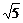 .
.
∴所求圆C的方程为(x-2)2+(y+3)2=5.
答案:(x-2)2+(y+3)2=5
3.(2004年全国卷Ⅲ,4)圆x2+y2-4x=0在点P(1, )处的切线方程为
)处的切线方程为
A.x+ y-2=0
B.x+
y-2=0
B.x+ y-4=0
y-4=0
C.x- y+4=0
D.x-
y+4=0
D.x- y+2=0
y+2=0
解法一:
 x2+y2-4x=0
x2+y2-4x=0
y=kx-k+
 x2-4x+(kx-k+
x2-4x+(kx-k+ )2=0.
)2=0.
该二次方程应有两相等实根,即Δ=0,解得k=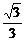 .
.
∴y- =
=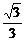 (x-1),即x-
(x-1),即x- y+2=0.
y+2=0.
解法二:∵点(1, )在圆x2+y2-4x=0上,
)在圆x2+y2-4x=0上,
∴点P为切点,从而圆心与P的连线应与切线垂直.
又∵圆心为(2,0),∴ ·k=-1.
·k=-1.
解得k=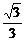 ,∴切线方程为x-
,∴切线方程为x- y+2=0.
y+2=0.
答案:D
2.圆x2+y2-4x+4y+6=0截直线x-y-5=0所得的弦长等于
A.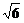 B.
B.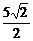 C.1 D.5
C.1 D.5
解析:圆心到直线的距离为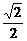 ,半径为
,半径为 ,弦长为2
,弦长为2 =
=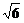 .
.
答案:A
1.(2005年北京海淀区期末练习题)设m>0,则直线 (x+y)+1+m=0与圆x2+y2=m的位置关系为
(x+y)+1+m=0与圆x2+y2=m的位置关系为
A.相切 B.相交
C.相切或相离 D.相交或相切
解析:圆心到直线的距离为d=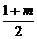 ,圆半径为
,圆半径为 .
.
∵d-r=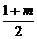 -
- =
=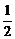 (m-2
(m-2 +1)=
+1)=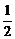 (
( -1)2≥0,
-1)2≥0,
∴直线与圆的位置关系是相切或相离.
答案:C
3.直线和圆相交,这类问题主要是求弦长以及弦的中点问题.
●点击双基
2.直线和圆相切,这类问题主要是求圆的切线方程.求圆的切线方程主要可分为已知斜率k或已知直线上一点两种情况,而已知直线上一点又可分为已知圆上一点和圆外一点两种情况.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com