
2.当直线和圆相切时,求切线方程一般要用圆心到直线的距离等于半径,求切线长一般要用切线、半径及圆外点与圆心连线构成的直角三角形;与圆相交时,弦长的计算也要用弦心距、半径及弦长的一半构成的直角三角形.
1.有关直线和圆的位置关系,一般要用圆心到直线的距离与半径的大小来确定.
2.解决直线与圆的位置关系的有关问题,往往充分利用平面几何中圆的性质使问题简化.
●教师下载中心
教学点睛
1.直线和圆的位置关系有且仅有三种:相离、相切、相交.判定方法有两个:几何法,比较圆心到直线的距离与圆的半径间的大小;代数法,看直线与圆的方程联立所得方程组的解的个数.
9.已知点P到两个定点M(-1,0)、N(1,0)距离的比为 ,点N到直线PM的距离为1,求直线PN的方程.
,点N到直线PM的距离为1,求直线PN的方程.
解:设点P的坐标为(x,y),
由题设有 =
= ,
,
即 =
= ·
·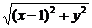 ,
,
整理得x2+y2-6x+1=0. ①
因为点N到PM的距离为1,|MN|=2,
所以∠PMN=30°,直线PM的斜率为±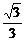 .
.
直线PM的方程为y=±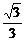 (x+1). ②
(x+1). ②
将②代入①整理得x2-4x+1=0.
解得x1=2+ ,x2=2-
,x2=2- .
.
代入②得点P的坐标为(2+ ,1+
,1+ )或(2-
)或(2- ,-1+
,-1+ );(2+
);(2+ ,-1-
,-1- )或(2-
)或(2- ,1-
,1- ).
).
直线PN的方程为y=x-1或y=-x+1.
●思悟小结
8.(文)求经过点A(-2,-4),且与直线l:x+3y-26=0相切于(8,6)的圆的方程.
解:设圆为x2+y2+Dx+Ey+F=0,依题意有方程组
 3D-E=-36,
3D-E=-36,
2D+4E-F=20,
8D+6E+F=-100.
|
 D=-11,
D=-11,
E=3,
F=-30.
∴圆的方程为x2+y2-11x+3y-30=0.
(理)已知点P是圆x2+y2=4上一动点,定点Q(4,0).
(1)求线段PQ中点的轨迹方程;
(2)设∠POQ的平分线交PQ于R,求R点的轨迹方程.
解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=1.
(2)设R(x,y),由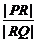 =
=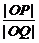 =
=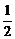 ,
,
设P(m,n),则有
 m=
m= ,
,
n= ,
,
代入x2+y2=4中,得
(x- )2+y2=
)2+y2= (y≠0).
(y≠0).
探究创新
7.方程ax2+ay2-4(a-1)x+4y=0表示圆,求a的取值范围,并求出其中半径最小的圆的方程.
解:(1)∵a≠0时,方程为[x- ]2+(y+
]2+(y+ )2=
)2=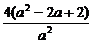 ,
,
由于a2-2a+2>0恒成立,
∴a≠0且a∈R时方程表示圆.
(2)r2=4·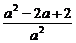 =4[2(
=4[2(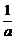 -
-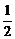 )2+
)2+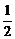 ],
],
∴a=2时,rmin2=2.
此时圆的方程为(x-1)2+(y-1)2=2.
6.已知M(x0,y0)是圆x2+y2=r2(r>0)内异于圆心的一点,则直线x0x+y0y=r2与此圆有何种位置关系?
分析:比较圆心到直线的距离与圆半径的大小.
解:圆心O(0,0)到直线x0x+y0y=r2的距离为d= .
.
∵P(x0,y0)在圆内,∴ <r.
<r.
则有d>r,故直线和圆相离.
培养能力
5.自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
解:圆(x-2)2+(y-2)2=1关于x轴的对称方程是(x-2)2+(y+2)2=1.
设l方程为y-3=k(x+3),由于对称圆心(2,-2)到l距离为圆的半径1,从而可得k1=- ,k2=-
,k2=- .故所求l的方程是3x+4y-3=0或4x+3y+3=0.
.故所求l的方程是3x+4y-3=0或4x+3y+3=0.
4.(2004年福建,13)直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于____________.
解析:由x2+y2-6x-2y-15=0,得(x-3)2+(y-1)2=25.
知圆心为(3,1),r=5.
由点(3,1)到直线x+2y=0的距离d= =
=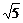 .
.
可得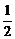 弦长为2
弦长为2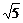 ,弦长为4
,弦长为4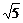 .
.
答案:4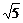
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com