5.点P在椭圆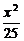
+
=1上，它到左焦点的距离是它到右焦点距离的两倍，则点P的横坐标是____________.
解析：利用第二定义.
答案：
●典例剖析
[例1] 已知F1为椭圆的左焦点，A、B分别为椭圆的右顶点和上顶点，P为椭圆上的点，当PF1⊥F1A，PO∥AB(O为椭圆中心)时，求椭圆的离心率.
剖析：求椭圆的离心率，即求
，只需求a、c的值或a、c用同一个量表示.本题没有具体数值，因此只需把a、c用同一量表示，由PF1⊥F1A，PO∥AB易得b=c，a=
b.
解：设椭圆方程为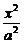
+
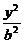=1(a＞b＞0)，F1(－c，0)，c2=a2－b2，
则P(－c，b
)，即P(－c，
).
∵AB∥PO，∴kAB=kOP，
即－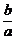
=
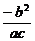.∴b=c.
又∵a=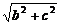
=b，
∴e==
=
.
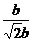评述：由题意准确画出图形，利用椭圆方程及直线平行与垂直的性质是解决本题的关键.
[例2] 如下图，设E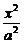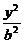：+=1(a＞b＞0)的焦点为F1与F2，且P∈E，∠F1PF2=2θ.
求证：△PF1F2的面积S=b2tanθ.
剖析：有些圆锥曲线问题用定义去解决比较方便.如本题，设|PF1|=r1，|PF2|=r2，则S=
r1r2sin2θ.若能消去r1r2，问题即获解决.
证明：设|PF1|=r1，|PF2|=r2，
则S=r1r2sin2θ，又|F1F2|=2c，
由余弦定理有
(2c)2=r12+r22－2r1r2cos2θ=(r1+r2)2－2r1r2－2r1r2cos2θ=(2a)2－2r1r2(1+cos2θ)，
于是2r1r2(1+cos2θ)=4a2－4c2=4b2.
所以r1r2=
.
这样即有S=·sin2θ=b2
=b2tanθ.
评述：解与△PF1F2(P为椭圆上的点)有关的问题，常用正弦定理或余弦定理，并结合|PF1|+|PF2|=2a来解决.
特别提示
我们设想点P在E上由A向B运动，由于△PF1F2的底边F1F2为定长，而高逐渐变大，故此时S逐渐变大.所以当P运动到点B时S取得最大值.由于b2为常数，所以tanθ逐渐变大.因2θ为三角形内角，故2θ∈(0，π)，θ∈(0，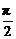
).这样，θ也逐渐变大，当P运动到B时，∠F1PF2取得最大值.故本题可引申为求最值问题，读者不妨一试.
[例3] 若椭圆ax2+by2=1与直线x+y=1交于A、B两点，M为AB的中点，直线OM(O为原点)的斜率为，且OA⊥OB，求椭圆的方程.
剖析：欲求椭圆方程，需求a、b，为此需要得到关于a、b的两个方程，由OM的斜率为.OA⊥OB，易得a、b的两个方程.
解：设A(x1，y1)，B(x2，y2)，M(
，
).
|
|
x+y=1，
ax2+by2=1，
∴=
，=1－=
.
∴M(，).
∵kOM=，∴b=a. ①
∵OA⊥OB，∴
·
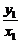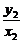=－1.
∴x1x2+y1y2=0.
∵x1x2=
，y1y2=(1－x1)(1－x2)，
∴y1y2=1－(x1+x2)+x1x2
=1－
+=
.
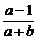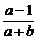∴+=0.
∴a+b=2. ②
由①②得a=2(－1)，b=2(－1).
∴所求方程为2(－1)x2+2(－1)y2=1.
评述：直线与椭圆相交的问题，通常采取设而不求，即设出A(x1，y1)，B(x2，y2)，但不是真的求出x1、y1、x2、y2，而是借助于一元二次方程根与系数的关系来解决问题.由OA⊥OB得x1x2+y1y2=0是解决本题的关键.
●闯关训练
夯实基础
4.如果方程x2+ky2=2表示焦点在y轴的椭圆，那么实数k的取值范围是____________.
解析：椭圆方程化为
+
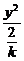=1.
焦点在y轴上，则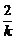
>2，即k<1.
又k>0，∴0<k<1.
答案：0＜k＜1
2.(2004年湖北，6)已知椭圆
+=1的左、右焦点分别为F1、F2，点P在椭圆上，若P、F1、F2是一个直角三角形的三个顶点，则点P到x轴的距离为
A.
B.3
C.
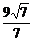D.
解析：由余弦定理判断∠P<90°，只能∠PF1F2或∠PF2F1为直角.由a=4，b=3得c=
，
∴|yP|=.
答案：D
|
|
x=4+5cos
，
y=3sin
A.(0，0)，(0，－8) B.(0，0)，(－8，0)
C.(0，0)，(0，8) D.(0，0)，(8，0)
解析：消参数得椭圆
+=1，
∴c=4.
易得焦点(0，0)，(8，0).
答案：D
1.(2003年北京宣武区模拟题)已知F1、F2是椭圆+=1的两个焦点，过F1的直线与椭圆交于M、N两点，则△MNF2的周长为
A.8 B.16 C.25 D.32
解析：利用椭圆的定义易知B正确.
答案：B
3.参数方程
方程
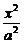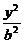+=1(a＞b＞0)，c=
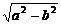，焦点是F1(－c，0)，F2(c，0)
2.
+
=1(a＞b＞0)，c=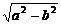，焦点是F1(0，－c)，F2(0，c)
|
y=bsinθ
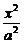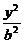+=1(a＞b＞0)∈(0，1)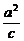
，l2：x=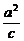思考讨论
对于焦点在y轴上的椭圆+=1(a＞b＞0)，其性质如何？焦半径公式怎样推导？
●点击双基
8.1 椭圆
●知识梳理
|
定义 |
1.到两个定点F1、F2的距离之和等于定长(＞|F1F2|)的点的轨迹 2.到定点F与到定直线l的距离之比等于常数e(∈(0，1))的点的轨迹 |
|
|