
9.(2003年春季北京)已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-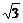 的直线与曲线M相交于A、B两点.
的直线与曲线M相交于A、B两点.
①问△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
②当△ABC为钝角三角形时,求这时点C的纵坐标的取值范围.
解:(1)依题意,曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为y2=4x,如下图.

(2)①由题意得,直线AB的方程为
y=-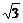 (x-1).
(x-1).
|
|
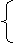 y=-
y=-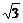 (x-1),
(x-1),
y2=4x,
解得A(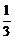 ,
,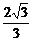 ),B(3,-2
),B(3,-2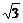 ),
),
若△ABC能为正三角形,
设C(-1,y),则|AC|=|AB|=|BC|,
|
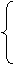 (
(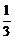 +1)2+(
+1)2+(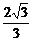 -y)2=(3-
-y)2=(3-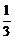 )2+(2
)2+(2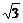 +
+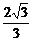 )2,
①
)2,
①
(3+1)2+(2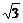 +y)2=(3-
+y)2=(3-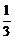 )2+(2
)2+(2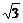 +
+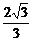 )2.
②
)2.
②
解得y=-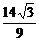 .
.
但y=-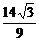 不符合(1),所以①②组成的方程组无解.因此直线l上不存在点C使△ABC是正三角形.
不符合(1),所以①②组成的方程组无解.因此直线l上不存在点C使△ABC是正三角形.
②设C(-1,y)使△ABC成钝角三角形,由
|
 y=-
y=-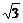 (x-1),
(x-1),
x=-1,
即当点C的坐标为(-1,2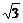 )时,A、B、C三点共线,故y≠2
)时,A、B、C三点共线,故y≠2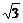 .
.
又|AC|2=(-1-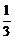 )2+(y-
)2+(y-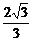 )2=
)2=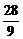 -
-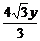 +y2,|BC|2=(3+1)2+(y+2
+y2,|BC|2=(3+1)2+(y+2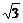 )2=28+4
)2=28+4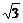 y+y2,|AB|2=(
y+y2,|AB|2=(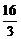 )2=
)2= .
.
当|BC|2>|AC|2+|AB|2,
即28+4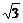 y+y2>
y+y2>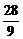 -
-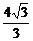 y+y2+
y+y2+ ,
,
即y>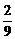
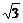 时,∠CAB为钝角.
时,∠CAB为钝角.
当|AC|2>|BC|2+|AB|2,
即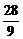 -
-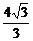 y+y2>28+4
y+y2>28+4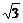 y+y2+
y+y2+ ,
,
即y<-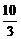
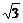 时,∠CBA为钝角.
时,∠CBA为钝角.
又|AB|2>|AC|2+|BC|2,即
 >
>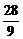 -
-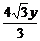 +y2+28+4
+y2+28+4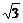 y+y2,即
y+y2,即
y2+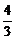
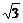 y+
y+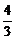 <0,(y+
<0,(y+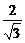 )2<0.
)2<0.
该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是
y<- 或y>
或y> (y≠2
(y≠2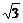 ).
).
●思悟小结
本节主要内容是抛物线的定义、方程及几何性质.解决本节问题时应注意以下几点:
8.过抛物线y2=2px(p>0)焦点F的弦AB,点A、B在抛物线准线上的射影为A1、B1,求∠A1FB1.
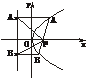
解:由抛物线定义及平行线性质知∠A1FB1=180°-(∠AFA1+∠BFB1)
=180°-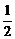 (180°-∠A1AF)-
(180°-∠A1AF)-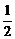 (180°-∠B1BF)
(180°-∠B1BF)
=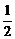 (∠A1AF+∠B1BF)=90°.
(∠A1AF+∠B1BF)=90°.
探究创新
7.给定抛物线y2=2x,设A(a,0),a>0,P是抛物线上的一点,且|PA|=d,试求d的最小值.
解:设P(x0,y0)(x0≥0),则y02=2x0,
∴d=|PA|=
= =
=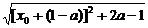 .
.
∵a>0,x0≥0,
∴(1)当0<a<1时,1-a>0,
此时有x0=0时,
dmin= =a.
=a.
(2)当a≥1时,1-a≤0,
此时有x0=a-1时,
dmin=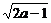 .
.
6.正方形ABCD中,一条边AB在直线y=x+4上,另外两顶点C、D在抛物线y2=x上,求正方形的面积.
解:设CD所在直线的方程为y=x+t,
|
|
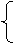 y=x+t,
y=x+t,
y2=x,
x2+(2t-1)x+t2=0,
∴|CD|=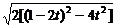
=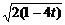 .
.
又直线AB与CD间距离为|AD|=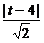 ,
,
∵|AD|=|CD|,
∴t=-2或-6.
从而边长为3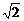 或5
或5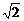 .
.
面积S1=(3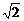 )2=18,S2=(5
)2=18,S2=(5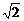 )2=50.
)2=50.
培养能力
5.下图所示的直角坐标系中,一运动物体经过点A(0,9),其轨迹方程是y=ax2+c(a<0),D=(6,7)为x轴上的给定区间.
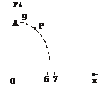
(1)为使物体落在D内,求a的取值范围;
(2)若物体运动时又经过点P(2,8.1),问它能否落在D内?并说明理由.
解:(1)把点A的坐标(0,9)代入y=ax2+c得c=9,即运动物体的轨迹方程为y=ax2+9.
令y=0,得ax2+9=0,即x2=-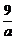 .
.
若物体落在D内,应有6<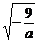 <7,
<7,
解得-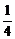 <a<-
<a<-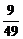 .
.
(2)若运动物体又经过点P(2,8.1),
则8.1=4a+9,解得a=-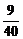 ,
,
∴-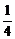 <-
<-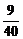 <-
<-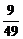 ,
,
∴运动物体能落在D内.
4.在抛物线y=4x2上求一点,使该点到直线y=4x-5的距离最短,该点的坐标是____________.
解法一:设与y=4x-5平行的直线y=4x+b与y=4x2相切,则y=4x+b代入y=4x2,得 4x2-4x-b=0. ①
Δ=16+16b=0时b=-1,代入①得x=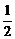 ,
,
∴所求点为(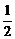 ,1).
,1).
解法二:设该点坐标为A(x0,y0),那么有y0=4x02.设点A到直线y=4x-5的距离为d,则
d=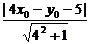 =
=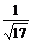 |-4x02+4x0-5|
|-4x02+4x0-5|
=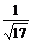 |4x02-4x0+5|=
|4x02-4x0+5|=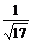 |4(x0-
|4(x0-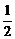 )2+1|.
)2+1|.
当且仅当x0=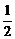 时,d有最小值,
时,d有最小值,
将x0=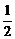 代入y=4x2解得y0=1.
代入y=4x2解得y0=1.
故A点坐标为(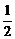 ,1).
,1).
答案:(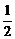 ,1)
,1)
3.(2003年春季上海)直线y=x-1被抛物线y2=4x截得线段的中点坐标是___________.
解析:将y=x-1代入抛物线y2=4x,经整理得x2-6x+1=0.
由韦达定理得x1+x2=6, =3,
=3,
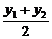 =
=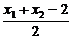 =
= =2.
=2.
∴所求点的坐标为(3,2).
答案:(3,2)
2.(2004年全国Ⅰ,8)设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是
A.[-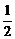 ,
,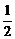 ]
B.[-2,2]
]
B.[-2,2]
C.[-1,1] D.[-4,4]
解析:∵y2=8x,∴Q(-2,0)(Q为准线与x轴的交点),设过Q点的直线l方程为y= k(x+2).
∵l与抛物线有公共点,
|
|
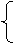 y2=8x,
y2=8x,
y=k(x+8)
即k2x2+(4k2-8)+4k2=0有解.
∴Δ=(4k2-8)2-16k4≥0,即k2≤1.
∴-1≤k≤1.
答案:C
1.(2003年高考·新课程)设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,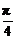 ],则P到曲线y=f(x)对称轴距离的取值范围为
],则P到曲线y=f(x)对称轴距离的取值范围为
A.[0,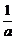 ]
B.[0,
]
B.[0,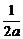 ]
]
C.[0,|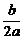 |]
D.[0,|
|]
D.[0,|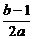 |]
|]
解析:tanα=k=f′(x)=2ax+b,
∴0≤2ax0+b≤1.
∴0≤x0+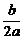 ≤
≤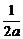 .
.
答案:B
5.(2002年全国)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;②焦点在x轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).
能使这抛物线方程为y2=10x的条件是____________.(要求填写合适条件的序号)
解析:由抛物线方程y2=10x可知②⑤满足条件.
答案:②⑤
●典例剖析
[例1] 求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
剖析:从方程形式看,求抛物线的标准方程仅需确定一个待定系数p;从实际分析,一般需确定p和确定开口方向两个条件,否则,应展开相应的讨论.
解:(1)设所求的抛物线方程为y2=-2px或x2=2py(p>0),
∵过点(-3,2),
∴4=-2p(-3)或9=2p·2.
∴p=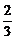 或p=
或p=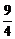 .
.
∴所求的抛物线方程为y2=-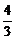 x或x2=
x或x2=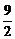 y,前者的准线方程是x=
y,前者的准线方程是x=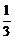 ,后者的准线方程是y=-
,后者的准线方程是y=-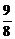 .
.
(2)令x=0得y=-2,令y=0得x=4,
∴抛物线的焦点为(4,0)或(0,-2).
当焦点为(4,0)时,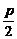 =4,
=4,
∴p=8,此时抛物线方程y2=16x;
焦点为(0,-2)时,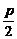 =2,
=2,
∴p=4,此时抛物线方程为x2=-8y.
∴所求的抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
评述:这里易犯的错误就是缺少对开口方向的讨论,先入为主,设定一种形式的标准方程后求解,以致失去一解.
[例2]如下图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=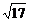 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
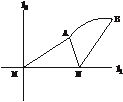
剖析:由题意所求曲线段是抛物线的一部分,求曲线方程需建立适当的直角坐标系,设出抛物线方程,由条件求出待定系数即可,求出曲线方程后要标注x、y的取值范围.
解:以直线l1为x轴,线段MN的垂直平分线为y轴,建立直角坐标系,由条件可知,曲线段C是以点N为焦点,以l2为准线的抛物线的一段.其中A、B分别为曲线段C的端点.
设曲线段C的方程为y2=2px(p>0)(xA≤x≤xB,y>0),其中xA、xB为A、B的横坐标,p=|MN|,
所以M(-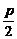 ,0)
、N(
,0)
、N(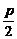 ,0).
,0).
由|AM|=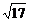 ,|AN|=3,得
,|AN|=3,得
(xA+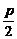 )2+2pxA=17, ①
)2+2pxA=17, ①
(xA-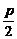 )2+2pxA=9. ②
)2+2pxA=9. ②
①②联立解得xA=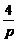 ,代入①式,并由p>0,
,代入①式,并由p>0,
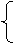
|
|
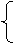 p=4, p=2,
p=4, p=2,
xA=1 xA=2.
因为△AMN为锐角三角形,所以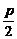 >xA.
>xA.
|
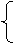
|
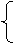 P=2, P=4,
P=2, P=4,
xA=2. xA=1.
由点B在曲线段C上,得xB=|BN|-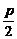 =4.
=4.
综上,曲线段C的方程为y2=8x(1≤x≤4,y>0).
评述:本题体现了坐标法的基本思路,考查了定义法、待定系数法求曲线方程的步骤,综合考查了学生分析问题、解决问题的能力.
[例3] 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.
剖析:证直线AC经过原点O,即证O、A、C三点共线,为此只需证kOC=kOA.本题也可结合图形特点,由抛物线的几何性质和平面几何知识去解决.
证法一:设AB:x=my+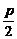 ,代入y2=2px,得y2-2pmy-P2=0.
,代入y2=2px,得y2-2pmy-P2=0.
由韦达定理,得yAyB=-p2,
即yB=-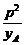 .
.
∵BC∥x轴,且C在准线x=-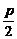 上,
上,
∴C(-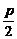 ,yB).
,yB).
则kOC=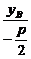 =
= =
=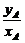 =kOA.
=kOA.
故直线AC经过原点O.
证法二:如下图,记准线l与x轴的交点为E,过A作AD⊥l,垂足为D.

则AD∥EF∥BC.连结AC交EF于点N,则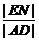 =
=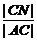 =
=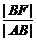 ,
,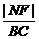 =
=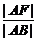 .
.
∵|AF|=|AD|,|BF|=|BC|,
∴|EN|=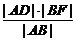 =
=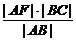 =|NF|,
=|NF|,
即N是EF的中点.从而点N与点O重合,故直线AC经过原点O.
评述:本题的“几何味”特别浓,这就为本题注入了活力.在涉及解析思想较多的证法中,关键是得到yA·yB=-p2这个重要结论.还有些证法充分利用了平面几何知识,这也提醒广大师生对圆锥曲线几何性质的重视,也只有这样才能挖掘出丰富多彩的解析几何的题目.
思考讨论
本题也可用平面向量来证明,读者不妨一试.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com