
8.5 轨迹问题
●知识梳理
本节主要内容是轨迹的概念及轨迹方程的求法.求轨迹方程常用的方法:(1)结合解析几何中某种曲线的定义,从定义出发寻找解决问题的方法;(2)利用几何性质,若所求的轨迹与图形的性质相关,往往利用三角形或圆的性质来解问题;(3)如果点P的运动轨迹或所在曲线已知,又点Q与点P之间的坐标可以建立某种关系,则借助点P的轨迹可以得到点Q的轨迹;(4)参数法.
●点击双基
3.涉及到圆锥曲线焦点弦的问题,还可以利用圆锥曲线的焦半径公式(即圆锥曲线的第二定义),应掌握求焦半径以及利用焦半径解题的方法.
拓展题例
[例1] (2003年福州市模拟题)已知抛物线C:y2=4(x-1),椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合.
(1)设B是椭圆C1短轴的一个端点,线段BF的中点为P,求点P的轨迹C2的方程;
(2)如果直线x+y=m与曲线C2相交于不同两点M、N,求m的取值范围.
(1)解法一:由y2=4(x-1)知抛物线C的焦点F坐标为(2,0).准线l的方程为x=0.设动椭圆C1的短轴的一个端点B的坐标为(x1,y1)(x1>2,y1≠0),点P(x,y),
|
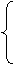
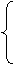
|
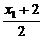 , x1=2x-2,
, x1=2x-2,
y= , y1=2y.
, y1=2y.
∴B(2x-2,2y)(x>2,y≠0).
设点B在准线x=0上的射影为点B′,椭圆的中心为点O′,则椭圆离心率e=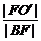 ,由
,由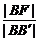 =
=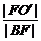 ,得
,得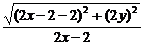 =
=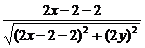 ,
,
整理,化简得y2=x-2(y≠0),这就是点P的轨迹方程.
解法二:抛物线y2=4(x-1)焦点为F(2,0),准线l:x=0.设P(x,y),
∵P为BF中点,
∴B(2x-2,2y)(x>2,y≠0).设椭圆C1的长半轴、短半轴、半焦距分别为a、b、c,
则c=(2x-2)-2=2x-4,b2=(2y)2=4y2,
∵(-c)-(-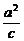 )=2,
)=2,
∴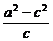 =2,
=2,
即b2=2c.∴4y2=2(2x-4),
即y2=x-2(y≠0),此即C2的轨迹方程.
|
|
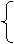 x+y=m,
x+y=m,
y2=x-2
m>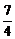 .
.
而当m=2时,直线x+y=2过点(2,0),这时它与曲线C2只有一个交点,
∴所求m的取值范围是(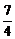 ,2)∪(2,+∞).
,2)∪(2,+∞).
[例2] 已知椭圆C: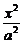 +
+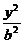 =1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A、B两点,设l与y轴交点为P,线段PF2的中点恰为B.
=1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A、B两点,设l与y轴交点为P,线段PF2的中点恰为B.
(1)若|k|≤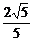 ,求椭圆C的离心率的取值范围;
,求椭圆C的离心率的取值范围;
(2)若k=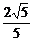 ,A、B到右准线距离之和为
,A、B到右准线距离之和为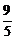 ,求椭圆C的方程.
,求椭圆C的方程.
解:(1)设右焦点F2(c,0),则l:y=k(x-c).
令x=0,则y=-ck,∴P(0,-ck).
∵B为F2P的中点,∴B(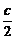 ,-
,-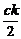 ).
).
∵B在椭圆上,∴ +
+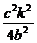 =1.
=1.
∴k2=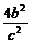 ·
·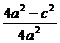 =(
=(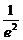 -1)(4-e2)
-1)(4-e2)
=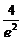 +e2-5.
+e2-5.
∵|k|≤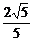 ,∴
,∴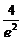 +e2-5≤
+e2-5≤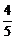 .
.
∴(5e2-4)(e2-5)≤0.
∴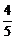 ≤e2<1.∴
≤e2<1.∴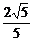 ≤e<1.
≤e<1.
(2)k=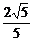 ,∴e=
,∴e=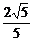 .∴
.∴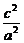 =
=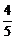 .
.
∴a2=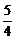 c2,b2=
c2,b2=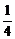 c2.椭圆方程为
c2.椭圆方程为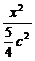 +
+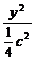 =1,即x2+5y2=
=1,即x2+5y2=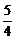 c2.
c2.
直线l方程为y=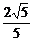 (x-c),
(x-c),
B(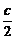 ,-
,-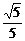 c),右准线为x=
c),右准线为x=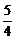 c.
c.
设A(x0,y0),则
(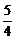 c-x0)+(
c-x0)+(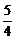 c-
c-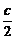 )=
)=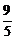 ,
,
∴x0=2c-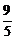 ,y0=
,y0=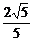 (c-
(c-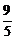 ).
).
∵A在椭圆上,
∴(2c-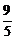 )2+5[
)2+5[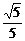 (c-
(c-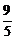 )]2=
)]2=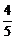 c2.
c2.
解之得c=2或c=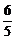 (不合题意,舍去).
(不合题意,舍去).
∴椭圆方程为x2+5y2=5,即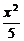 +y2=1.
+y2=1.
2.涉及直线与圆锥曲线相交弦的问题,主要有这样几个方面:相交弦的长,有弦长公式|AB|=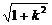 |x2-x1|;弦所在直线的方程(如中点弦、相交弦等)、弦的中点的轨迹等,这可以利用“设点代点、设而不求”的方法(设交点坐标,将交点坐标代入曲线方程,并不具体求出坐标,而是利用坐标应满足的关系直接导致问题的解决).
|x2-x1|;弦所在直线的方程(如中点弦、相交弦等)、弦的中点的轨迹等,这可以利用“设点代点、设而不求”的方法(设交点坐标,将交点坐标代入曲线方程,并不具体求出坐标,而是利用坐标应满足的关系直接导致问题的解决).
1.直线与圆锥曲线有无公共点或有几个公共点的问题,可以转化为它们所对应的方程构成的方程组是否有解或解的个数问题,往往通过消元最终归结为讨论一元二次方程根的情况.需要注意的是当直线平行于抛物线的对称轴或双曲线的渐近线时,直线与抛物线或双曲线有且只有一个交点.
3.求圆锥曲线的弦长时,可利用弦长公式
d=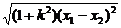 =
=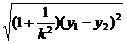 .
.
再结合韦达定理解决.焦点弦的长也可以直接利用焦半径公式处理,可以使运算简化.
●教师下载中心
教学点睛
2.涉及弦的中点问题,除利用韦达定理外,也可以运用平方差法,但必须以直线与圆锥曲线相交为前提,否则不宜用此法.
1.解决直线和圆锥曲线的位置关系问题时,对于消元后的一元二次方程,必须讨论二次项的系数和判别式Δ,有时借助图形的几何性质更为方便.
9.(2003年北京)如下图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为 M(0,r)(b>r>0).
(1)写出椭圆的方程,求椭圆的焦点坐标及离心率.
(2)直线y=k1x交椭圆于两点C(x1,y1),D(x2,y2)(y2>0);直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4)(y4>0).
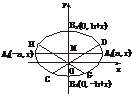
求证: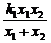 =
=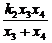 .
.
(3)对于(2)中的C、D、G、H,设CH交x轴于点P,GD交x轴于点Q.
求证:|OP|=|OQ|.
(证明过程不考虑CH或GD垂直于x轴的情形)
(1)解: 椭圆方程为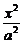 +
+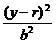 =1.
=1.
焦点坐标为F1(-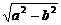 ,r),F2(
,r),F2(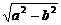 ,r),
,r),
离心率e=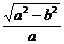 .
.
(2)证明:将直线CD的方程y=k1x代入椭圆方程,得b2x2+a2(k1x-r)2=a2b2,
整理得(b2+a2k12)x2-2k1a2rx+(a2r2-a2b2)=0.
根据韦达定理,得
x1+x2=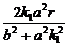 ,x1x2=
,x1x2=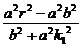 ,
,
所以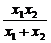 =
=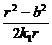 . ①
. ①
将直线GH的方程y=k2x代入椭圆方程,同理可得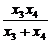 =
=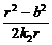 ②
②
由①②得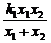 =
= =
=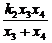 .
.
所以结论成立.
(3)证明:设点P(p,0),点Q(q,0).
由C、P、H三点共线,得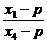 =
=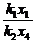 ,
,
解得p=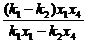 .
.
由D、Q、G三点共线,同理可得q=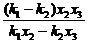 .
.

由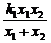 =
=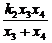 变形得-
变形得-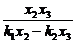 =
=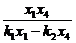 ,
,
即-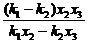 =
=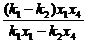 .
.
所以|p|=|q|,即|OP|=|OQ|.
●思悟小结
8.已知直线y=(a+1)x-1与曲线y2=ax恰有一个公共点,求实数a的值.
|
|
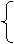 y=(a+1)x-1,
y=(a+1)x-1,
y2=ax,
|
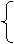 x=1,
x=1,
y=0.
(2)当a≠0时,方程组化为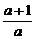 y2-y-1=0.
y2-y-1=0.
|
 x=-1,
x=-1,
y=-1.
|
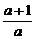 ≠0,即a≠-1,令Δ=0,得1+4·
≠0,即a≠-1,令Δ=0,得1+4·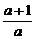 =0,解得a=-
=0,解得a=-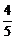 ,这时方程组恰有
,这时方程组恰有
x=-5,
y=-2.
综上所述,可知当a=0,-1,-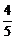 时,直线与曲线恰有一个公共点.
时,直线与曲线恰有一个公共点.
探究创新
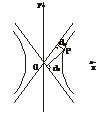
7.试证明双曲线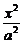 -
-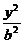 =1(a>0,b>0)上任意一点到它的两条渐近线的距离之积为常数.
=1(a>0,b>0)上任意一点到它的两条渐近线的距离之积为常数.
证明:设P(x0,y0)是已知双曲线上任意一点,双曲线的渐近线为bx±ay=0,则点P到两渐近线的距离之积为d1·d2=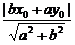 ·
·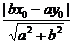 =
=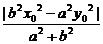 =
=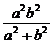 = 常数.
= 常数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com