6.注意参数的取值范围对方程的影响.

●教师下载中心

教学点睛

5.如果轨迹动点P(x，y)的坐标之间的关系不易找到，也没有相关点可用时，可先考虑将x、y用一个或几个参数来表示，消去参数得轨迹方程，此法称为参数法.参数法中常选变角、变斜率等为参数.

4.如果轨迹动点P(x，y)依赖于另一动点Q(a，b)，而Q(a，b)又在某已知曲线上，则可先列出关于x、y、a、b的方程组，利用x、y表示出a、b，把a、b代入已知曲线方程便得动点P的轨迹方程.此法称为代入法.

3.如果能够确定动点的轨迹满足某种已知曲线的定义，则可用曲线定义写出方程，这种方法称为定义法.

2.如果题目中的条件有明显的等量关系，或者可以利用平面几何知识推出等量关系，求方程时可用直接法.

1.求轨迹方程的一般步骤是：建系、设点、列式、代入、化简、检验.检验就是要检验点的轨迹的纯粹性和完备性.

9.(2004年春季安徽)已知k＞0，直线l₁：y=kx，l₂：y=－kx.

(1)证明：到l₁、l₂的距离的平方和为定值a(a＞0)的点的轨迹是圆或椭圆；

(2)求到l₁、l₂的距离之和为定值c(c＞0)的点的轨迹.

(1)证明：设点P(x，y)为动点，则

+=a，

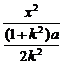整理得+=1.

因此，当k=1时，动点的轨迹为圆；

当k≠1时，动点的轨迹为椭圆.

(2)解：设点P(x，y)为动点，则

|y－kx|+|y+kx|=c.

当y≥k|x|时，y－kx+y+kx=c，

即y=c；

当y≤－k|x|时，kx－y－y－kx=c，即y=－c；

当－k|x|＜y＜k|x|，x＞0时，kx－y+y+kx=c，即x=c；

当－k|x|＜y＜k|x|，x＜0时，y－kx－y－kx=c，即x=－c.

综上，动点的轨迹为矩形.

●思悟小结

8.过抛物线y²=4x的焦点的直线l与抛物线交于A、B两点，O为坐标原点.求△AOB的重心G的轨迹C的方程.

解：抛物线的焦点坐标为(1，0)，当直线l不垂直于x轴时，设方程为y=k(x－1)，代入y²=4x，

得k²x²－x(2k²+4)+k²=0.

设l方程与抛物线相交于两点，

∴k≠0.设点A、B的坐标分别为(x₁，y₁)、(x₂，y₂)，

根据韦达定理，有x₁+x₂=，

从而y₁+y₂=k(x₁+x₂－2)=.

设△AOB的重心为G(x，y)，

消去k，得x=+(y)2，

y==，

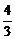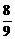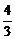∴y²=x－.当l垂直于x轴时，A、B的坐标分别为(1，2)和(1，－2)，△AOB的重心G(，0)，也适合y²=x－，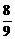

因此所求轨迹C的方程为y²=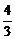x－.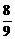

探究创新

7.AB是圆O的直径，且｜AB｜＝2a，M为圆上一动点，作MN⊥AB，垂足为N，在OM上取点P，使｜OP｜＝｜MN｜，求点P的轨迹.

解：以圆心O为原点，AB所在直线为x轴建立直角坐标系(如下图)，则⊙O的方程为x²+y²＝a²，设点P坐标为(x，y)，并设圆与y轴交于C、D两点，作PQ⊥AB于Q，则有＝.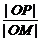

∵｜OP｜＝｜MN｜，

∴｜OP｜²＝｜OM｜·｜PQ｜.

∴x²+y²＝a｜y｜，即　 x²+(y±)²＝()².

轨迹是分别以CO、OD为直径的两个圆.

6.求经过定点A(1，2)，以x轴为准线，离心率为的椭圆下方的顶点的轨迹方程.

解：设椭圆下方的焦点F(x₀，y₀)，由定义=，

∴|AF|=1，即点F的轨迹方程为(x₀－1)²+(y₀－2)²=1.

又设椭圆下方顶点为P(x，y)，则x₀=x，y₀=y，

∴点P的轨迹方程是(x－1)²+(y－2)²=1.

培养能力