
2.如下图,花坛水池中央有一喷泉,水管OP=1 m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面2 m,P距抛物线对称轴1 m,则在水池直径的下列可选值中,最合算的是

A.2.5 m B.4 m
C.5 m D.6 m
解析:以O为原点,OP所在直线为y轴建立直角坐标系(如下图),则抛物线方程可设为

y=a(x-1)2+2,P点坐标为(0,1),
∴1=a+2.∴a=-1.
∴y=-(x-1)2+2.
令y=0,得(x-1)2=2,∴x=1±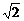 .
.
∴水池半径OM=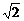 +1≈2.414(m).
+1≈2.414(m).
因此水池直径约为2×|OM|=4.828(m).
答案:C
1.1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了两颗“铱星”系统通信卫星.卫星运行的轨道是以地球中心为一个焦点的椭圆,近地点为m km,远地点为 n km,地球的半径为R km,则通信卫星运行轨道的短轴长等于
A.2
B. 
C.2mn
D.mn
|
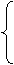
 -c=m+R, ①
-c=m+R, ①
 +c=n+R,
②
+c=n+R,
②
∴c=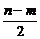 ,
,
2b=2
=2 .
.
答案:A
5.在相距1400 m的A、B两哨所,听到炮弹爆炸声音的时间相差3 s,已知声速340 m/s.炮弹爆炸点所在曲线的方程为________________.
解析:设M(x,y)为曲线上任一点,
则|MA|-|MB|=340×3=1020<1400.
∴M点轨迹为双曲线,且a= =510,
=510,
c= =700.
=700.
∴b2=c2-a2=(c+a)(c-a)=1210×190.
∴M点轨迹方程为 -
-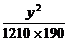 =1.
=1.
答案: -
-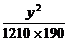 =1
=1
●典例剖析
[例1] 设有一颗彗星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此彗星离地球相距m万千米和 m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为
m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为 和
和 ,求该彗星与地球的最近距离.
,求该彗星与地球的最近距离.
剖析:本题的实际意义是求椭圆上一点到焦点的距离,一般的思路:由直线与椭圆的关系,列方程组解之;或利用定义法抓住椭圆的第二定义求解.同时,还要注意结合椭圆的几何意义进行思考.仔细分析题意,由椭圆的几何意义可知:只有当该彗星运行到椭圆的较近顶点处时,彗星与地球的距离才达到最小值即为a-c,这样把问题就转化为求a,c或a-c.
解:建立如下图所示直角坐标系,设地球位于焦点F(-c,0)处,椭圆的方程为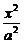 +
+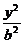 =1,
=1,
当过地球和彗星的直线与椭圆的长轴夹角为 时,由椭圆的几何意义可知,彗星A只能满足∠xFA=
时,由椭圆的几何意义可知,彗星A只能满足∠xFA= (或∠xFA′=
(或∠xFA′= ).
).

作AB⊥Ox于B,则|FB|=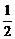 |FA|=
|FA|= m,
m,
故由椭圆的第二定义可得
 m=
m= (
( -c), ①
-c), ①
 m=
m= (
( -c+
-c+ m). ②
m). ②
两式相减得 m=
m= ·
· m,∴a=2c.
m,∴a=2c.
代入①,得m=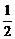 (4c-c)=
(4c-c)=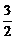 c,
c,
∴c= m.∴a-c=c=
m.∴a-c=c= m.
m.
答:彗星与地球的最近距离为 m万千米.
m万千米.
评述: (1)在天体运行中,彗星绕恒星运行的轨道一般都是椭圆,而恒星正是它的一个焦点,该椭圆的两个端点,一个是近地点,另一个则是远地点,这两点到恒星的距离一个是a-c,另一个是a+c.
(2)以上给出的解答是建立在椭圆的概念和几何意义之上的,以数学概念为根基充分体现了数形结合的思想.另外,数学应用问题的解决在数学化的过程中也要时刻不忘审题,善于挖掘隐含条件,有意识地训练数学思维的品质.
思考讨论
椭圆上任一点到焦点的距离的最大值和最小值是多少?怎样证明?
提示:利用焦半径易求得最大值为a+c,最小值为a-c.
[例2] 某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如下图所示).已知PA=100 m,PB=150 m,∠APB=60°,试说明怎样运土最省工.

剖析:首先抽象为数学问题,半圆中的点可分为三类:(1)沿AP到P较近;(2)沿BP到P较近;(3)沿AP、BP到P同样远.
显然,第三类点是第一、二类的分界点,设M是分界线上的任意一点.则有|MA|+|PA|=|MB|+|PB|.
于是|MA|-|MB|=|PB|-|PA|=150-100=50.
从而发现第三类点M满足性质:点M到点A与点B的距离之差等于常数50,由双曲线定义知,点M在以A、B为焦点的双曲线的右支上,故问题转化为求此双曲线的方程.
解:以AB所在直线为x轴,线段AB的中点为原点建立直角坐标系xOy,设M(x,y)是沿AP、BP运土同样远的点,则
|MA|+|PA|=|MB|+|PB|,
∴|MA|-|MB|=|PB|-|PA|=50.
在△PAB中,由余弦定理得
|AB|2=|PA|2+|PB|2-2|PA||PB|cos60°=17500,且50<|AB|.由双曲线定义知M点在以A、B为焦点的双曲线右支上,设此双曲线方程为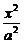 -
-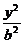 =1(a>0,b>0).
=1(a>0,b>0).
|
 2a=50,
2a=50,
4c2=17500,
c2=a2+b2,
|
 a2=625,
a2=625,
b2=3750.
∴M点轨迹是 -
- =1(x≥25)在半圆内的一段双曲线弧.于是运土时将双曲线左侧的土沿AP运到P处,右侧的土沿BP运到P处最省工.
=1(x≥25)在半圆内的一段双曲线弧.于是运土时将双曲线左侧的土沿AP运到P处,右侧的土沿BP运到P处最省工.
评述:(1)本题是不等量与等量关系问题,涉及到分类思想,通过建立直角坐标系,利用点的集合性质,构造圆锥曲线模型(即分界线)从而确定出最优化区域.
(2)应用分类思想解题的一般步骤:①确定分类的对象;②进行合理的分类;③逐类逐级讨论;④归纳各类结果.
[例3] 根据我国汽车制造的现实情况,一般卡车高3 m,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m的距离行驶.已知拱口AB宽恰好是拱高OC的4倍,若拱宽为a m,求能使卡车安全通过的a的最小整数值.
剖析:根据问题的实际意义,卡车通过隧道时应以卡车沿着距隧道中线0.4 m到2 m间的道路行驶为最佳路线,因此,卡车能否安全通过,取决于距隧道中线2 m(即在横断面上距拱口中点2 m)处隧道的高度是否够3 m,据此可通过建立坐标系,确定出抛物线的方程后求得.
解:如下图,以拱口AB所在直线为x轴,以拱高OC所在直线为y轴建立直角坐标系,由题意可得抛物线的方程为x2=-2p(y- ),
),
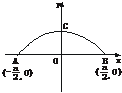
∵点A(- ,0)在抛物线上,
,0)在抛物线上,
∴(- )2=-2p(0-
)2=-2p(0- ),得p=
),得p= .
.
∴抛物线方程为x2=-a(y- ).
).
取x=1.6+0.4=2,代入抛物线方程,得
22=-a(y- ),y=
),y= .
.
由题意,令y>3,得 >3,
>3,
∵a>0,∴a2-12a-16>0.
∴a>6+2 .
.
又∵a∈Z,∴a应取14,15,16,….
答:满足本题条件使卡车安全通过的a的最小正整数为14 m.
评述: 本题的解题过程可归纳为两步:一是根据实际问题的意义,确定解题途径,得到距拱口中点2 m处y的值;二是由y>3通过解不等式,结合问题的实际意义和要求得到a的值,值得注意的是这种思路在与最佳方案有关的应用题中是常用的.
●闯关训练
夯实基础
4.探照灯反射镜的纵断面是抛物线的一部分,光源在抛物线的焦点,已知灯口直径是 60 cm,灯深40 cm,则光源到反射镜顶点的距离是____________ cm.
解析:设抛物线方程为y2=2px(p>0),点(40,30)在抛物线y2=2px上,
∴900=2p×40.∴p= .∴
.∴ =
= .因此,光源到反射镜顶点的距离为
.因此,光源到反射镜顶点的距离为 cm.
cm.
答案:
3.天安门广场,旗杆比华表高,在地面上,观察它们顶端的仰角都相等的各点所在的曲线是
A.椭圆 B.圆
C.双曲线的一支 D.抛物线
解析:设旗杆高为m,华表高为n,m>n.旗杆与华表的距离为2a,以旗杆与地面的交点和华表与地面的交点的连线段所在直线为x轴、垂直平分线为y轴建立直角坐标系.设曲线上任一点M(x,y),由题意 =
= ,即(m2-n2)x2+(m2-n2)y2-2a(m2-n2)x+ (m2-n2)a2=0.
,即(m2-n2)x2+(m2-n2)y2-2a(m2-n2)x+ (m2-n2)a2=0.
答案:B
2.某抛物线形拱桥的跨度是20 m,拱高是4 m,在建桥时每隔4 m需用一柱支撑,其中最长的支柱是
A.4 m B.3.84 m C.1.48 m D.2.92 m
解析:建立适当坐标系,设抛物线方程为x2=-2py(p>0),由题意知其过定点(10, -4),代入x2=-2py,得p= .
.
∴x2=-25y.当x0=2时,y0= ,∴最长支柱长为4-|y0|=4-
,∴最长支柱长为4-|y0|=4- =3.84(m).
=3.84(m).
答案:B
1.一抛物线型拱桥,当水面离桥顶2 m时,水面宽4 m,若水面下降1 m时,则水面宽为
A. m
B.2
m
B.2 m C.4.5
m
D.9 m
m C.4.5
m
D.9 m
解析:建立适当的直角坐标系,设抛物线方程为x2=-2Py(P>0),由题意知,抛物线过点(2,-2),
∴4=2p×2.∴p=1.∴x2=-2y.
当y0=-3时,得x02=6.
∴水面宽为2|x0|=2 .
.
答案:B
8.6 圆锥曲线的应用
●知识梳理
解析几何在日常生活中应用广泛,如何把实际问题转化为数学问题是解决应用题的关键,而建立数学模型是实现应用问题向数学问题转化的常用方法.本节主要通过圆锥曲线在实际问题中的应用,说明数学建模的方法,理解函数与方程、等价转化、分类讨论等数学思想.
●点击双基
2.在探求轨迹的过程中,需要注意的是轨迹的“完备性”和“纯粹性”,也就是说既不能多,也不能少,因此,在求得轨迹方程之后,要深入地再思考一下:①是否还遗漏了一些点?是否还有另一个满足条件的轨迹方程存在?②在所求得的轨迹方程中,x、y的取值范围是否有什么限制?
拓展题例
[例1] 是否存在同时满足下列条件的抛物线?若存在,求出它的方程;若不存在,请说明理由.
(1)准线是y轴;
(2)顶点在x轴上;
(3)点A(3,0)到此抛物线上动点P的距离最小值是2.
解:假设存在这样的抛物线,顶点为(a,0),则方程为y2=4a(x-a)(a≠0),
设P(x0,y0),则y02=4a(x0-a),
|AP|2=(x0-3)2+y02
=[x0-(3-2a)]2+12a-8a2,
令f(a)=|AP|2,
①当a>0时,有x0≥a,
当3-2a≥a即a∈(0,1]时,
|AP|2=f(3-2a),∴a=1或a= ;
;
抛物线方程为y2=4(x-1)或y2=2(x- ).
).
当3-2a<a即a>1时,|AP|2=f(a).
∴a=5或a=1(舍),
抛物线方程为y2=20(x-5).
②当a<0时,显然与已知矛盾,
∴所求抛物线方程为y2=4(x-1)或y2=2(x- )或y2=20(x-5).
)或y2=20(x-5).
[例2] (2003年太原市模拟题)已知椭圆的焦点为F1(-1,0)、F2(1,0),直线x=4是它的一条准线.
(1)求椭圆的方程;
(2)设A1、A2分别是椭圆的左顶点和右顶点,P是椭圆上满足|PA1|-|PA2|=2的一点,求tan∠A1PA2的值;
(3)若过点(1,0)的直线与以原点为顶点、A2为焦点的抛物线相交于点M、N,求MN中点Q的轨迹方程.
解:(1)设椭圆方程为 +
+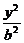 =1(a>b>0).
=1(a>b>0).
|
 c=1,
c=1,
 =4,
=4,
|
|
 c=1,
c=1,
a=2,
所求椭圆方程为 +
+ =1.
=1.
(2)由题设知,点P在以A1、A2为焦点,实轴长为2的双曲线的右支上.
由(1)知A1(-2,0),A2(2,0),
设双曲线方程为 -
- =1(m>0,n>0).
=1(m>0,n>0).
|


|
m2+n2=4,
n= .
.
∴双曲线方程为x2- =1.由
=1.由

 +
+ =1,
=1,
x2- =1,
=1,
解得P点的坐标为( ,
, )或(
)或( ,-
,- ).当P点坐标为(
).当P点坐标为( ,
, )时,tan∠A1PA2=
)时,tan∠A1PA2= =-4
=-4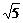 .
.
同理当P点坐标为( ,-
,-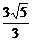 )时,
)时,
tan∠A1PA2=-4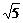 .
.
故tan∠A1PA2=-4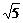 .
.
(3)由题设知,抛物线方程为y2=8x.
设M(x1,y1)、N(x2,y2),MN的中点Q(x,y),
当x1≠x2时,有
 y12=8x1,
①
y12=8x1,
①
y22=8x2, ②
x= ,
③
,
③
y= ,
④
,
④
 =
= .
⑤
.
⑤
①-②,得 (y1+y2)=8,
(y1+y2)=8,
将④⑤代入上式,有 ·2y=8,
·2y=8,
即y2=4(x-1)(x≠1).
当x1=x2时,MN的中点为(1,0),仍满足上式.
故所求点Q的轨迹方程为y2=4(x-1).
1.已知曲线求方程或已知方程画曲线是解析几何中的两个基本问题.如何探求动点的轨迹方程呢?①从定义出发,还本索源.在探求动点的轨迹方程时,如能结合解析几何中某种曲线的定义,也就能寻找到解决问题的钥匙;②利用平面几何的性质.动点的轨迹与图形的性质相关,若某些轨迹与直线或圆有关,则可以利用三角形或圆的性质来帮助分析;③伴随曲线的思想和方法.如果点P的运动轨迹或所在的曲线已知,又点P与点Q的坐标之间可以建立起某种关系,则借助于点P的运动轨迹,我们便可以得到点Q的运动轨迹,这便是伴随曲线的思想方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com