
3.(2005年启东市第二次调研)设P1( ,
, )、P2(-
)、P2(- ,-
,- ),M是双曲线y=
),M是双曲线y= 上位于第一象限的点,对于命题①|MP2|-|MP1|=2
上位于第一象限的点,对于命题①|MP2|-|MP1|=2 ;②以线段MP1为直径的圆与圆x2+y2=2相切;③存在常数b,使得M到直线y=-x+b的距离等于
;②以线段MP1为直径的圆与圆x2+y2=2相切;③存在常数b,使得M到直线y=-x+b的距离等于 |MP1|.其中所有正确命题的序号是____________.
|MP1|.其中所有正确命题的序号是____________.
解析:由双曲线定义可知①正确,②画图由题意可知正确,③由距离公式及|MP1|可知正确.
答案:①②③
2.已知F1(-3,0)、F2(3,0)是椭圆 +
+ =1的两个焦点,P是椭圆上的点,当∠F1PF2=
=1的两个焦点,P是椭圆上的点,当∠F1PF2= 时,△F1PF2的面积最大,则有
时,△F1PF2的面积最大,则有
A.m=12,n=3 B.m=24,n=6
C.m=6,n= D.m=12,n=6
D.m=12,n=6
解析:由条件求出椭圆方程即得m=12,n=3.
答案:A
1.(2005年北京东城区目标检测)以正方形ABCD的相对顶点A、C为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为
A. B.
B.
C. D.
D.
解析:建立坐标系,设出椭圆方程,由条件求出椭圆方程,可得e= .
.
答案:D
5.(2004年春季北京)若直线mx+ny-3=0与圆x2+y2=3没有公共点,则m、n满足的关系式为____________;以(m,n)为点P的坐标,过点P的一条直线与椭圆 +
+ =1的公共点有____________个.
=1的公共点有____________个.
解析:将直线mx+ny-3=0变形代入圆方程x2+y2=3,消去x,得
(m2+n2)y2-6ny+9-3m2=0.
令Δ<0得m2+n2<3.
又m、n不同时为零,
∴0<m2+n2<3.
由0<m2+n2<3,可知|n|< ,|m|<
,|m|< ,
,
再由椭圆方程a=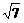 ,b=
,b= 可知公共点有2个.
可知公共点有2个.
答案:0<m2+n2<3 2
●典例剖析
[例1] (2005年春季北京,18)如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点.

(1)写出直线l的截距式方程;
(2)证明: +
+ =
= ;
;
(3)当a=2p时,求∠MON的大小.
剖析:易知直线l的方程为 +
+ =1,欲证
=1,欲证 +
+ =
= ,即求
,即求 的值,为此只需求直线l与抛物线y2=2px交点的纵坐标.由根与系数的关系易得y1+y2、y1y2的值,进而证得
的值,为此只需求直线l与抛物线y2=2px交点的纵坐标.由根与系数的关系易得y1+y2、y1y2的值,进而证得 +
+ =
= .由
.由 ·
· =0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
=0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
(1)解:直线l的截距式方程为 +
+ =1. ①
=1. ①
(2)证明:由①及y2=2px消去x可得by2+2pay-2pab=0. ②
点M、N的纵坐标y1、y2为②的两个根,故y1+y2=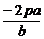 ,y1y2=-2pa.
,y1y2=-2pa.
所以 +
+ =
= =
= =
= .
.
(3)解:设直线OM、ON的斜率分别为k1、k2,
则k1= ,k2=
,k2= .
.
当a=2p时,由(2)知,y1y2=-2pa=-4p2,
由y12=2px1,y22=2px2,相乘得(y1y2)2=4p2x1x2,
x1x2= =
= =4p2,
=4p2,
因此k1k2= =
= =-1.
=-1.
所以OM⊥ON,即∠MON=90°.
评述:本题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力.
[例2] (2005年黄冈高三调研考题)已知椭圆C的方程为 +
+ =1(a>b>0),双曲线
=1(a>b>0),双曲线 -
- =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如下图)
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如下图)

(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当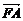 =λ
=λ 时,求λ的最大值.
时,求λ的最大值.
剖析:(1)求椭圆方程即求a、b的值,由l1与l2的夹角为60°易得 =
= ,由双曲线的距离为4易得a2+b2=4,进而可求得a、b.
,由双曲线的距离为4易得a2+b2=4,进而可求得a、b.
(2)由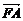 =λ
=λ ,欲求λ的最大值,需求A、P的坐标,而P是l与l1的交点,故需求l的方程.将l与l2的方程联立可求得P的坐标,进而可求得点A的坐标.将A的坐标代入椭圆方程可求得λ的最大值.
,欲求λ的最大值,需求A、P的坐标,而P是l与l1的交点,故需求l的方程.将l与l2的方程联立可求得P的坐标,进而可求得点A的坐标.将A的坐标代入椭圆方程可求得λ的最大值.
解:(1)∵双曲线的渐近线为y=± x,两渐近线夹角为60°,
x,两渐近线夹角为60°,
又 <1,
<1,
∴∠POx=30°,即 =tan30°=
=tan30°= .
.
∴a= b.
b.
又a2+b2=4,
∴a2=3,b2=1.
故椭圆C的方程为 +y2=1.
+y2=1.
(2)由已知l:y= (x-c),与y=
(x-c),与y= x解得P(
x解得P( ,
, ),
),
由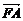 =λ
=λ 得A(
得A( ,
,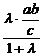 ).
).
将A点坐标代入椭圆方程得
(c2+λa2)2+λ2a4=(1+λ)2a2c2.
∴(e2+λ)2+λ2=e2(1+λ)2.
∴λ2=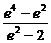 =-[(2-e2)+
=-[(2-e2)+ ]+3≤3-2
]+3≤3-2 .
.
∴λ的最大值为 -1.
-1.
评述:本题考查了椭圆、双曲线的基础知识,及向量、定比分点公式、重要不等式的应用.解决本题的难点是通过恒等变形,利用重要不等式解决问题的思想.本题是培养学生分析问题和解决问题能力的一道好题.
[例3] 设椭圆中心是坐标原点,长轴在x轴上,离心率e= ,已知点P(0,
,已知点P(0, )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是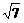 ,求这个椭圆方程,并求椭圆上到点P的距离等于
,求这个椭圆方程,并求椭圆上到点P的距离等于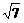 的点的坐标.
的点的坐标.
剖析:设椭圆方程为 +
+ =1,由e=
=1,由e= 知椭圆方程可化为x2+4y2=4b2,然后将距离转化为y的二次函数,二次函数中含有一个参数b,在判定距离有最大值的过程中,要讨论y=-
知椭圆方程可化为x2+4y2=4b2,然后将距离转化为y的二次函数,二次函数中含有一个参数b,在判定距离有最大值的过程中,要讨论y=- 是否在y的取值范围内,最后求出椭圆方程和P点坐标.
是否在y的取值范围内,最后求出椭圆方程和P点坐标.
解法一:设所求椭圆的直角坐标方程是 +
+ =1,其中a>b>0待定.
=1,其中a>b>0待定.
由e2= =
=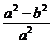 =1-(
=1-( )2可知
)2可知 =
= =
= =
= ,即a=2b.
,即a=2b.
设椭圆上的点(x,y)到点P的距离为d,则d2=x2+(y- )2=a2(1-
)2=a2(1- )+y2-3y+
)+y2-3y+ = 4b2-3y2-3y+
= 4b2-3y2-3y+ =-3(y+
=-3(y+ )2+4b2+3,其中-b≤y≤b.
)2+4b2+3,其中-b≤y≤b.
如果b< ,则当y=-b时d2(从而d)有最大值,由题设得(
,则当y=-b时d2(从而d)有最大值,由题设得(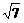 )2=(b+
)2=(b+ )2,由此得b=
)2,由此得b=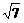 -
- >
> ,与b<
,与b< 矛盾.
矛盾.
因此必有b≥ 成立,于是当y=-
成立,于是当y=- 时d2(从而d)有最大值,由题设得(
时d2(从而d)有最大值,由题设得(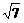 )2=4b2+3,由此可得b=1,a=2.
)2=4b2+3,由此可得b=1,a=2.
故所求椭圆的直角坐标方程是 +y2=1.
+y2=1.
由y=- 及求得的椭圆方程可得,椭圆上的点(-
及求得的椭圆方程可得,椭圆上的点(- ,-
,- ),点(
),点( ,-
,- )到点P的距离都是
)到点P的距离都是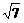 .
.
解法二:根据题设条件,设椭圆的参数方程是
|
 x=acosθ,
x=acosθ,
y=bsinθ,
∵e= ,
,
∴a=2b.
设椭圆上的点(x,y)到点P的距离为d,则
d2=x2+(y- )2=a2cos2θ+(bsinθ-
)2=a2cos2θ+(bsinθ- )2=-3b2·(sinθ+
)2=-3b2·(sinθ+ )2+4b2+3.
)2+4b2+3.
如果 >1,即b<
>1,即b< ,则当sinθ=-1时,d2(从而d)有最大值,由题设得(
,则当sinθ=-1时,d2(从而d)有最大值,由题设得(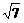 )2=(b+
)2=(b+ ) 2,由此得b=
) 2,由此得b=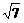 -
- >
> ,与b<
,与b< 矛盾.
矛盾.
因此必有 ≤1成立,于是当sinθ=-
≤1成立,于是当sinθ=- 时,d2(从而d)有最大值,由题设得(
时,d2(从而d)有最大值,由题设得(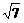 )2=4b2+3.
)2=4b2+3.

|
y=sinθ.
消去参数得 +y2=1,由sinθ=
+y2=1,由sinθ=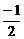 ,cosθ=±
,cosθ=± 知椭圆上的点(-
知椭圆上的点(- ,-
,- ),(
),( ,-
,- )到P点的距离都是
)到P点的距离都是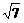 .
.
评述:本题体现了解析几何与函数、三角知识的横向联系,解答中要注意讨论.
深化拓展
根据图形的几何性质,以P为圆心,以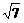 为半径作圆,圆与椭圆相切时,切点与P的距离为
为半径作圆,圆与椭圆相切时,切点与P的距离为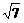 ,此时的椭圆和切点即为所求.读者不妨一试.
,此时的椭圆和切点即为所求.读者不妨一试.
|
 x2+(y-
x2+(y- )2=7,
)2=7,
x2+4y2=4b2,
得3y2+3y- =4b2-7,
=4b2-7,
由Δ=0得b2=1,
即椭圆方程为x2+4y2=4.
所求点为(- ,-
,- )、(
)、( ,-
,- ).
).
●闯关训练
夯实基础
4.(2005年春季上海,7)双曲线9x2-16y2=1的焦距是____________.
解析:将双曲线方程化为标准方程得 -
- =1.∴a2=
=1.∴a2= ,b2=
,b2= ,
,
c2=a2+b2= +
+ =
= .
.
∴c= ,2c=
,2c= .
.
答案:
3.若点(x,y)在椭圆4x2+y2=4上,则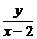 的最小值为
的最小值为
A.1 B.-1
C.-
 D.以上都不对
D.以上都不对
解析: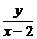 的几何意义是椭圆上的点与定点(2,0)连线的斜率.显然直线与椭圆相切时取得最值,设直线y=k(x-2)代入椭圆方程(4+k2)x2-4k2x+4k2-4=0.
的几何意义是椭圆上的点与定点(2,0)连线的斜率.显然直线与椭圆相切时取得最值,设直线y=k(x-2)代入椭圆方程(4+k2)x2-4k2x+4k2-4=0.
令Δ=0,k=±
 .
.
∴kmin=-
 .
.
答案:C
2.到两定点A(0,0),B(3,4)距离之和为5的点的轨迹是
A.椭圆 B.AB所在直线
C.线段AB D.无轨迹
解析:数形结合易知动点的轨迹是线段AB:y= x,其中0≤x≤3.
x,其中0≤x≤3.
答案:C
1.(2005年春季北京,5)设abc≠0,“ac>0”是“曲线ax2+by2=c为椭圆”的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
解析:ac>0 曲线ax2+by2=c为椭圆.
曲线ax2+by2=c为椭圆.
反之成立.
答案:B
8.7 圆锥曲线的综合问题
●知识梳理
解析几何是联系初等数学与高等数学的纽带,它本身侧重于形象思维、推理运算和数形结合,综合了代数、三角、几何、向量等知识.反映在解题上,就是根据曲线的几何特征准确地转换为代数形式,根据方程画出图形,研究几何性质.学习时应熟练掌握函数与方程的思想、数形结合的思想、参数的思想、分类与转化的思想等,以达到优化解题的目的.
具体来说,有以下三方面:
(1)确定曲线方程,实质是求某几何量的值;含参数系数的曲线方程或变化运动中的圆锥曲线的主要问题是定值、最值、最值范围问题,这些问题的求解都离不开函数、方程、不等式的解题思想方法.有时题设设计的非常隐蔽,这就要求认真审题,挖掘题目的隐含条件作为解题突破口.
(2)解析几何也可以与数学其他知识相联系,这种综合一般比较直观,在解题时保持思维的灵活性和多面性,能够顺利进行转化,即从一知识转化为另一知识.
(3)解析几何与其他学科或实际问题的综合,主要体现在用解析几何知识去解有关知识,具体地说就是通过建立坐标系,建立所研究曲线的方程,并通过方程求解来回答实际问题.在这一类问题中“实际量”与“数学量”的转化是易出错的地方,这是因为在坐标系中的量是“数量”,不仅有大小还有符号.
●点击双基
0.0022v2+6274.3275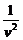 -17.4375=0,
-17.4375=0,
解得v≈19.44 m/s或v≈86.88 m/s.
若v≈86.88 m/s,则x=156.246 m,与题目不符,
而v≈19.44 m/s,符合题意,为所求解.
故v≈19.44 m/s=69.984 km/h≈70 km/h.
答:骑手沿跑道飞出时的速度应为70 km/h.
评述:本题直接构造y是x的函数解析式很困难,应引入适当的参数(时间t)作媒介,再研究x与y是怎样随参数变化而变化的,问题往往就容易解决了.这种辅助变量的引入要具体问题具体分析,以解题的简捷为原则.
[例2] A、B、C是我方三个炮兵阵地,A在B正东6 km,C在B正北偏西30°,相距4 km,P为敌炮阵地,某时刻A处发现敌炮阵地的某种信号,由于B、C两地比A距P地远,因此4 s后,B、C才同时发现这一信号,此信号的传播速度为1 km/s,A若炮击P地,求炮击的方位角.
解:如下图,以直线BA为x轴,线段BA的中垂线为y轴建立坐标系,则

B(-3,0)、A(3,0)、C(-5,2 ).
).
因为|PB|=|PC|,所以点P在线段BC的垂直平分线上.
因为kBC=- ,BC中点D(-4,
,BC中点D(-4, ),
),
所以直线PD的方程为y- =
= (x+4). ①
(x+4). ①
又|PB|-|PA|=4,故P在以A、B为焦点的双曲线右支上.
设P(x,y),则双曲线方程为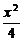 -
-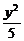 =1(x≥0). ②
=1(x≥0). ②
联立①②,得x=8,y=5 ,
,
所以P(8,5 ).因此kPA=
).因此kPA= =
= .
.
故炮击的方位角为北偏东30°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com