
9.(2004年天津,理19)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD;
(3)求二面角C-PB-D的大小.

解法一:(1)证明:连结AC交BD于O.连结EO.
∵底面ABCD是正方形,∴点O是AC的中点.
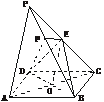
在△PAC中,EO是中位线,
∴PA∥EO.
而EO 平面EDB且PA
平面EDB且PA 平面EDB,
平面EDB,
∴PA∥平面EDB.
(2)证明:∵PD⊥底面ABCD且DC 底面ABCD,∴PD⊥DC.
底面ABCD,∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形.而DE是斜边PC的中线,
∴DE⊥PC. ①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC.
而DE 平面PDC,∴BC⊥DE. ②
平面PDC,∴BC⊥DE. ②
由①和②推得DE⊥平面PBC.
而PB 平面PBC,∴DE⊥PB.
平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD.
(3)解:由(2)知PB⊥DF,故∠EFD是二面角C-PB-D的平面角.
由(2)知,DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,则PD=DC=a,BD= a,
a,
PB= =
= a,
a,
PC= =
= a,
a,
DE= PC=
PC= a.
a.
在Rt△PDB中,
DF= =
= =
= a.
a.
在Rt△EFD中,
sin∠EFD= =
= =
= ,
,
∴∠EFD= .
.
∴二面角C-PB-D的大小为 .
.
解法二:如图所示建立空间直角坐标系,D为坐标原点.设DC=a.

(1)证明:连结AC交BD于G.连结EG.
依题意得A(a,0,0),P(0,0,a),E(0,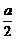 ,
,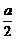 ).
).
∵底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为(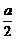 ,
,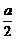 ,0)且
,0)且 =(a,0,-a),
=(a,0,-a),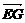 =(
=(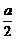 ,0,-
,0,-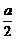 ).
).
∴ =2
=2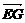 .这表明PA∥EG.
.这表明PA∥EG.
而EG 平面EDB且PA
平面EDB且PA 平面EDB,
平面EDB,
∴PA∥平面EDB.
(2)证明:依题意得B(a,a,0),
 =(a,a,-a).
=(a,a,-a).
又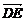 =(0,
=(0,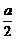 ,
,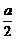 ),
),
故 ·
·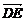 =0+
=0+ -
- =0.
=0.
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,
∴PB⊥平面EFD.
(3)解:设点F的坐标为(x0,y0,z0), =λ
=λ ,则(x0,y0,z0-a)=λ(a,a,-a).
,则(x0,y0,z0-a)=λ(a,a,-a).
从而x0=λa,y0=λa,z0=(1-λ)a.
∴ =(-x0,
=(-x0,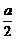 -y0,
-y0,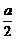 -z0)=[-λa,(
-z0)=[-λa,( -λ)a,(λ-
-λ)a,(λ- )a].
)a].
由条件EF⊥PB知 ·
· =0,即
=0,即
-λa2+( -λ)a2-(λ-
-λ)a2-(λ- )a2=0,
)a2=0,
解得λ=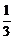 .
.
∴点F的坐标为( ,
, ,
,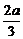 ),且
),且 =(-
=(- ,
, ,-
,- ),
), =(-
=(- ,-
,- ,-
,-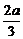 ).∴
).∴ ·
· =-
=-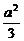 -
-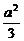 +
+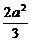 =0,即PB⊥FD.
=0,即PB⊥FD.
故∠EFD是二面角C-PB-D的平面角.
∵ ·
· =
= -
- +
+ =
= ,且|
,且| |=
|= ·a,|
·a,| |=
|= ·a,
·a,
∴cos∠EFD= =
= .
.
∴∠EFD= .∴二面角C-PB-D为
.∴二面角C-PB-D为 .
.
●思悟小结
8.(2005年春季北京,文16)如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.求:

(1)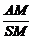 的值;
的值;
(2)二面角S-BC-A的大小;
(3)正三棱锥S-ABC的体积.
解:(1)∵SB=SC,AB=AC,M为BC的中点,∴SM⊥BC,AM⊥BC.

由棱锥的侧面积等于底面积的2倍,即
3× BC×SM=2×
BC×SM=2× BC×AM,
BC×AM,
得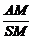 =
=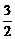 .
.
(2)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,GM=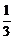 AM.
AM.
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S-BC-A的平面角.
在Rt△SGM中,
∵SM= AM=
AM= ×3GM=2GM,
×3GM=2GM,
∴∠SMA=∠SMG=60°,
即二面角S-BC-A的大小为60°.
(3)∵△ABC的边长是3,
∴AM= ,GM=
,GM= ,SG=GMtan60°=
,SG=GMtan60°= ·
· =
= 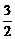 .
.
∴VS-ABC=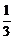 S
S ·SG=
·SG=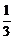 ·
·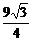 ·
·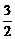 =
= .
.
(2005年春季北京,理16)如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于B1、C1.将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M.求:

(1)二面角A1-B1C1-M的大小;
(2)异面直线A1B1与CC1所成角的大小.(用反三角函数表示)
解:(1)连结AM、A1G.

∵G是正三角形ABC的中心,且M为BC的中点,
∴A、G、M三点共线,AM⊥BC.
∵B1C1∥BC,∴B1C1⊥AM于点G,
即GM⊥B1C1,GA1⊥B1C1.
∴∠A1GM是二面角A1-B1C1-M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,∠A1MG=90°.
在Rt△A1GM中,由A1G=AG=2GM,得∠A1GM=60°,
即二面角A1-B1C1-M的大小是60°.
(2)过B1作C1C的平行线交BC于点P,则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得B1P=C1C=1=BP,PM=BM-BP= ,A1B1=AB1=2.
,A1B1=AB1=2.
∵A1M⊥面BB1C1C于点M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1G·sin60°= ·
· =
=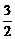 .
.
在Rt△A1MP中,A1P2=A1M2+PM2=(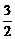 )2+(
)2+( )2=
)2= .
.
在△A1B1P中,由余弦定理得
cos∠A1B1P=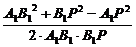 =
= =
= ,
,
∴异面直线A1B1与CC1所成角的大小为arccos .
.
探究创新
7.在正三棱柱ABC-A1B1C1中,AB1= BB1,
BB1,
(1)求证:AB1⊥BC1;
(2)求二面角A-BC1-C的正切值.
(1)证法一:如图,取BC的中点M,连结B1M、BC1交于N,则AM⊥面BC1.下证BC1⊥B1M.设BB1=1,则AB1= ,AB=BC=
,AB=BC= ,
,

∴tan∠B1MB= =tan∠B1BC1.
=tan∠B1BC1.
∴得△B1MB∽△B1BN.
∴∠B1BM=90°=∠B1NB,即BC1⊥B1M.
∴BC1⊥斜线AB1.
证法二:如图,取B1C1和B1B的中点E与D,连结ED,则DE∥BC1.再取AB的中点G,连结DG,则DG∥AB1,

∴∠GDE为异面直线AB1、BC1所成的角.下用勾股定理证明∠GDE为直角.取A1B1的中点F,连结EF、EG、FG,则EG= 且DE、DG均可表示出.
且DE、DG均可表示出.
故可知EG2=DE2+DG2,∴∠GDE=90°.
(2)解:连结AN,则∠ANM为所求二面角的平面角,tan∠ANM=3.
评述:本题(1)证法一中可把面BB1C1C单独拿出作成平面图形,则易于观察△B1MB与△B1NB的相似关系.证法二的特点是思路较好.因为所证为两异面直线,作出其所成角为一般方法.
6.(2003年春季北京)如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2 ,侧棱长为4,E、F分别为棱AB、BC的中点,EF∩BD=G.
,侧棱长为4,E、F分别为棱AB、BC的中点,EF∩BD=G.

(1)求证:平面B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d.
(1)证法一:连结AC.
∵正四棱柱ABCD-A1B1C1D1的底面是正方形,∴AC⊥BD.又AC⊥D1D,∴AC⊥平面BDD1B1.
∵E、F分别为AB、BC的中点,故EF∥AC.
∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
证法二:∵BE=BF,∠EBD=∠FBD=45°,
∴EF⊥BD.
又EF⊥D1D,∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
(2)在对角面BDD1B1中,作D1H⊥B1G,垂足为H.
∵平面B1EF⊥平面BDD1B1,且平面B1EF∩平面BDD1B1=B1G,
∴D1H⊥平面B1EF,且垂足为H.
∴点D1到平面B1EF的距离d=D1H.
解法一:在Rt△D1HB1中,
D1H=D1B1·sin∠D1B1H.

∵D1B1= A1B1=
A1B1= ·2
·2 =4,
=4,
sin∠D1B1H=sin∠B1GB= =
=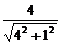 =
= ,
,
∴d=D1H=4· =
= .
.
解法二:∵△D1HB1∽△B1BG,
∴ =
=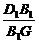 .
.
∴d=D1H= =
=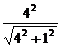 =
= .
.
解法三:连结D1G,则△D1GB1的面积等于正方形DBB1D1面积的一半,即 ·B1G·D1H=
·B1G·D1H= B1B2,
B1B2,

∴d=D1H= =
=  .
.
培养能力
5.三棱锥一条侧棱长是16 cm,和这条棱相对的棱长是18 cm,其余四条棱长都是17 cm,求棱锥的体积.
解:如图,取AD的中点E,连结CE、BE,

∵AC=CD=17,DE=8,CE2=172-82=225,BE=CE,
∴取BC的中点F,连结EF,EF为BC边上的高,EF= =
= =12.
=12.
∴S =108.
=108.
∵AC=CD=17cm,E为AD的中点,CE⊥AD,同理BE⊥AD,
∴DA⊥平面BCE.
∴三棱锥可分为以底面BCE为底,以AE、DE为高的两个三棱锥.
∴VA-BCD=VA-BCE+VD-BCE=2·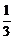 S
S ·AE=2×
·AE=2×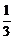 ×108×8=576(cm3).
×108×8=576(cm3).
4.在三棱锥S-ABC中,∠ASB=∠ASC=∠BSC=60°,则侧棱SA与侧面SBC所成的角的大小是_____________.
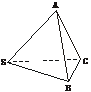
答案:arccos
3.在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH的边及其内部运动,则M只需满足条件__________时,就有MN⊥AC.
答案:点M与F重合
说明:本题答案不唯一,当点M在线段FH上时均有MN⊥AC.
2.P是长方体AC1上底面A1C1内任一点,设AP与三条棱AA1、AB、AD所成的角为α、β、γ,则cos2α+cos2β+cos2γ的值是
A.1 B.2 C.
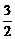 D.不确定正
D.不确定正
解析:以AP为一条对角线截得小长方体AP,由长方体的对角线长定理可得cos2α+cos2β
+cos2γ=1.
答案:A
1.(2004年全国Ⅰ,10)已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则 等于
等于
A. B.
B.
 C.
C.
 D.
D.
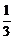
解析:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,

∴四面体EFGH也是正四面体.
连结AE并延长与CD交于点M,
连结AG并延长与BC交于点N.
∵E、G分别为面的中心,
∴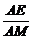 =
= =
= .∴
.∴ =
= .
.
又∵MN= BD,∴
BD,∴ =
=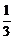 .
.
∵面积比是相似比的平方,∴ =
= .
.
答案:A
5.过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为__________.
解析:由锥体平行于底面的截面性质知,自上而下三锥体的侧面积之比,S侧1∶S侧2∶S侧3=
1∶4∶9,所以锥体被分成三部分的侧面积之比为1∶3∶5.
答案:1∶3∶5
●典例剖析
[例1] 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.

解法一:连结A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,
∵EF∥A1C1,
∴A1C1∥平面B1EDF.∴C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.
∵平面B1D1D⊥平面B1EDF,
∴O1H⊥平面B1EDF,即O1H为棱锥的高.
∵△B1O1H∽△B1DD1,
∴O1H= =
= a,
a,
V =
=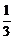 S
S ·O1H=
·O1H=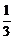 ·
· ·EF·B1D·O1H=
·EF·B1D·O1H=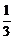 ·
· ·
· a·
a· a·
a· a=
a=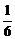 a3.
a3.
解法二:连结EF,设B1到平面C1EF的距离为h1,D到平面C1EF的距离为h2,则h1+h2=B1D1= a,∴V
a,∴V =V
=V +V
+V =
=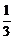 ·S
·S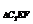 ·(h1+h2)=
·(h1+h2)=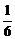 a3.
a3.
解法三:V =V
=V -V
-V -V
-V =
=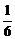 a3.
a3.
特别提示
求体积常见方法有:①直接法(公式法);②分割法;③补形法.
[例2] 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=2,BC=a,又侧棱PA⊥底面ABCD.
(1)当a为何值时,BD⊥平面PAC?试证明你的结论.
(2)当a=4时,求D点到平面PBC的距离.
(3)当a=4时,求直线PD与平面PBC所成的角.
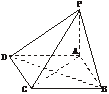
剖析:本题主要考查棱锥的性质,直线、平面所成的角的计算和点到平面的距离等基础知识.同时考查空间想象能力、逻辑推理能力和计算能力.
本题主要是在有关的计算中,推理得到所求的问题,因而尽量选择用坐标法计算.
解:(1)以A为坐标原点,以AD、AB、AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,当a=2时,BD⊥AC,又PA⊥BD,故BD⊥平面PAC.故a=2.
(2)当a=4时,D(4,0,0)、C(0,2,0)、C(4,2,0)、P(0,0,2)、 =(0,2,-2),
=(0,2,-2), =(4,0,0).
=(4,0,0).
设平面PBC的法向量为n,则n· =0,n·
=0,n· =0,即(x,y,z)·(0,2,-2)=0,(x,y,z)·(4,0,0)=0,得x=0,y=z,取y=1,故n=(0,1,1).则D点到平面PBC的距离d=
=0,即(x,y,z)·(0,2,-2)=0,(x,y,z)·(4,0,0)=0,得x=0,y=z,取y=1,故n=(0,1,1).则D点到平面PBC的距离d= =
= .
.
(3)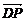 =(4,0,2),cos〈
=(4,0,2),cos〈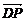 ,n〉=
,n〉=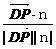 =
=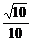 >0,证〈
>0,证〈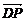 ,n〉=α,设直线PD与平面PBC所成的角为θ,则sinθ=sin(
,n〉=α,设直线PD与平面PBC所成的角为θ,则sinθ=sin( -α)=cosα=
-α)=cosα=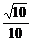 .
.
所以直线PD与平面PBC所成的角为arcsin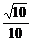 .
.
[例3] 如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.
(1)求证:S-ABC为正三棱锥;
(2)已知SA=a,求S-ABC的全面积.
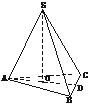
(1)证明:正棱锥的定义中,底面是正多边形;顶点在底面上的射影是底面的中心,两个条件缺一不可.作三棱锥S-ABC的高SO,O为垂足,连结AO并延长交BC于D.
因为SA⊥BC,所以AD⊥BC.又侧棱与底面所成的角都相等,从而O为△ABC的外心,OD为BC的垂直平分线,所以AB=AC.又∠BAC=60°,故△ABC为正三角形,且O为其中心.所以S-ABC为正三棱锥.
(2)解:只要求出正三棱锥S-ABC的侧高SD与底面边长,则问题易于解决.在Rt△SAO中,由于SA=a,∠SAO=60°,所以SO= a,AO=
a,AO= a.因O为重心,所以AD=
a.因O为重心,所以AD=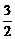 AO=
AO= a,BC=2BD=2ADcot60°=
a,BC=2BD=2ADcot60°= a,OD=
a,OD=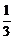 AD=
AD= a.
a.
在Rt△SOD中,SD2=SO2+OD2=( a)2+(
a)2+( a)2=
a)2= ,则SD=
,则SD= a.
a.
于是,(SS-ABC)全= ·(
·( a)2sin60°+3·
a)2sin60°+3· ·
· a·
a· a=
a=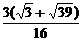 a2.
a2.
深化拓展
(1)求正棱锥的侧面积或全面积还可以利用公式S正棱锥底=cosα·S正棱锥侧(α为侧面与底面所成的二面角).就本题cosα= ,S
,S =
= a2,所以(SS-ABC)侧=
a2,所以(SS-ABC)侧= a2÷
a2÷ =
= a2.于是也可求出全面积.
a2.于是也可求出全面积.
(2)注意到高SO= a,底面边长BC=
a,底面边长BC= a是相等的,因此这类正三棱锥还有高与底面边长相等的性质,反之亦真.
a是相等的,因此这类正三棱锥还有高与底面边长相等的性质,反之亦真.
(3)正三棱锥中,若侧棱与底面边长相等,则变成四个面都是正三角形的三棱锥,这时可称为正四面体,因此正四面体是特殊的正三棱锥,但正三棱锥不一定是正四面体.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com