
9.12 球
●知识梳理
2.理解多面体、正多面体、凸多面体的概念,熟悉五种正多面体.
●教师下载中心
教学点睛
学习本节要使学生理解多面体、正多面体的概念.
拓展题例
[例1] 正方体ABCD-A1B1C1D1中,异面直线CD1和BC1所成的角是
A.60° B.45° C.90° D.120°
解析:连结D1A1、AC,知△ACD1是等边三角形,且D1A∥BC1,所以BC1与CD1所成的角是60°.
答案:A
[例2] 边长为a的正三角形,要拼接成一个正三棱柱且不剩料,应如何设计?(在图中用虚线画出)

解:设O为△ABC的中心,连结OA、OB、OC,并设OA、OB、OC的中点分别为A1、B1、C1,过A1、B1、C1分别向三边作垂线,则所得三个矩形即为三个侧面,三个角上的小四边形拼在一起即为上底面.
[变式] △ABC若为一般三角形,又如何拼接?
[例3] 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱A1B1和B1C1的中点.
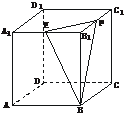
(1)求二面角B1-BF-E的大小.
(2)求点D到平面BEF的距离.
(3)能否在棱B1B上找到一点M,使DM⊥面BEF?若能,请确定点M的位置;若不能,请说明理由.
解:(1)过B1作B1G⊥BF于G,连结EG,则由EB1⊥面B1BCC1,可知EG⊥BF.

∴∠B1GE是二面角B1-BF-E的平面角.
在Rt△BB1F中,B1B=a,B1F= ,
,
∴BF= =
= a,
a,
B1G=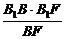 =
= =
=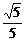 a.
a.
在Rt△B1GE中,B1E= ,B1G=
,B1G=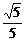 a,
a,
∴tan∠B1GE=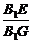 =
=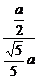 =
= .
.
∴∠B1GE=arctan .
.
故二面角B1-BF-E的大小为arctan .
.
(2)连结B1D1与EF交于N,
则EF⊥B1D1.又BB1⊥EF,
∴EF⊥面BB1D1D.又EF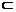 面BEF,
面BEF,
∴面BEF⊥面BB1D1D,且面BEF∩面BB1D1D=BN.
过D作DH⊥BN于H,则DH⊥面BEF.
∴DH的长即为点D到面BEF的距离.
在矩形BB1D1D中,
易证△BDH∽△NBB1,
∴ =
= ,DH=
,DH= =
=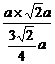 =
= a.故点D到面BEF的距离为
a.故点D到面BEF的距离为 a.
a.
(3)在平面BB1D1D中,延长DH交BB1于M,由(2),DH⊥面BEF,
∴DM⊥面BEF.
由△BDM∽△B1BN,有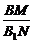 =
=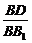 ,
,
∴BM= =
= =
= .
.
则M为BB1的中点.
故在棱BB1上可找到点M,使DM⊥面BEF,此时M为BB1的中点.
1.割补法是求多面体体积的常用方法.
5.(2003年烟台诊断性测试)(B)正方体ABCD-A1B1C1D1的棱长为2,且AC与BD交于点O,E为棱DD1的中点,以A为原点,建立空间直角坐标系A-xyz,如图所示.
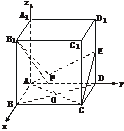
(1)求证:B1O⊥平面EAC;
(2)若点F在EA上且B1F⊥AE,试求点F的坐标;
(3)求二面角B1-EA-C的正弦值.
(1)证明:由题设知下列各点的坐标:
A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),E(0,2,1),B1(2,0,2).
由于O是正方形ABCD的中心,
∴O(1,1,0).
∴ =(-1,1,-2),
=(-1,1,-2), =(2,2,0),
=(2,2,0),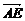 =(0,2,1).
=(0,2,1).
∴ ·
· =(-1,1,-2)·(2,2,0)=-1·2+1·2-2·0=0,
=(-1,1,-2)·(2,2,0)=-1·2+1·2-2·0=0,
 ·
·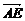 =(-1,1,-2)·(0,2,1)=-1·0+1·2-2·1=0.
=(-1,1,-2)·(0,2,1)=-1·0+1·2-2·1=0.
∴ ⊥
⊥ ,
, ⊥
⊥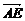 .
.
∴B1O⊥平面ACE.
(2)解:设点F的坐标为F(0,y,z),则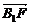 =(-2,y,z-2),
=(-2,y,z-2),
∵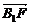 ⊥
⊥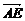 ,
,
∴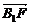 ·
·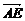 =(-2,y,z-2)·(0,2,1)=2y+z-2=0. ①
=(-2,y,z-2)·(0,2,1)=2y+z-2=0. ①
又∵点F在AE上,∴ =λ
=λ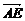 (λ∈R).
(λ∈R).
又 =(0,y,z),
=(0,y,z),
∴(0,y,z)=λ(0,2,1)=(0,2λ,λ).
于是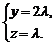 ②
②
由①②可得λ= ,y=
,y= ,z=
,z= ,
,
∴F(0, ,
, ).
).
(3)解:∵B1O⊥平面EAC,B1F⊥AE,连结OF,由三垂线定理的逆定理得OF⊥AE,
∴∠OFB1即为二面角B1-EA-C的平面角.
∵| |=
|= =
= ,
,
又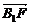 =(-2,
=(-2, ,-
,-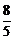 ),
),
∴|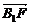 |=
|=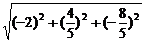 =
=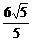 .
.
在Rt△B1OF中,sin∠B1FO= =
= .
.
故二面角B1-EA-C的正弦值为 .
.
●思悟小结
4.(文)已知正方体ABCD-A1B1C1D1的棱长为2,O为AC与BD的交点,M为DD1的中点.

(1)求证:直线B1O⊥平面MAC;
(2)求二面角B1-MA-C的大小.
(1)证明:∵BB1⊥平面ABCD,OB⊥AC,
∴B1O⊥AC.
连结MO、MB1,则MO=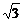 ,B1O=
,B1O= ,MB1=3.
,MB1=3.
∵MO2+B1O2=MB12,∴∠MOB1=90°.
∴B1O⊥MO.
∵MO∩AC=O,∴B1O⊥平面MAC.
(2)解:作ON⊥AM于点N,连结B1N.
∵B1O⊥平面MAC,∴AM⊥平面B1ON.
∴B1N⊥AM.
∴∠B1NO就是二面角B1-MA-C的平面角.
∵AM=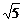 ,CM=
,CM=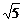 ,∴AM=CM.
,∴AM=CM.
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=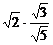 =
= 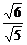 .
.
在Rt△B1ON中,tan∠B1NO=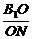 =
=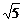 ,
,
∴∠B1NO=arctan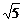 ,即所求二面角的大小为arctan
,即所求二面角的大小为arctan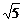 .
.
说明:本题的两问是递进式的,第(1)问是为第(2)问作铺垫的.第(2)问中构造二面角的平面角的方法是典型的三垂线法.
(理)在边长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB与C1D1的中点.
(1)求证:四边形A1ECF是菱形;
(2)求证:EF⊥平面A1B1C;
(3)求A1B1与平面A1ECF所成角的正切值.
(1)证明:取A1B1的中点G,连结C1G、GE.
∵A1G∥FC1且A1G=FC1,∴A1GC1F是平行四边形.∴A1F∥C1G.同理C1G∥CE.∴A1F∥CE.由勾股定理算得A1E=A1F=CE=CF= a,∴四边形A1ECF是菱形.
a,∴四边形A1ECF是菱形.
(2)证明:连结C1B,∵E、F分别为AB与C1D1的中点,∴C1F=BE.又C1F∥BE,
∴C1FEB为平行四边形.∴C1B∥EF.而C1B⊥B1C,∴EF⊥B1C.又四边形A1ECF是菱形,∴EF⊥A1C.∴EF⊥面A1B1C.
(3)解:由(2)知,EF⊥平面A1B1C,又EF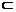 平面A1ECF,∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.∴∠B1A1C就是A1B1与平面A1ECF所成的角.
平面A1ECF,∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.∴∠B1A1C就是A1B1与平面A1ECF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=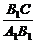 =
= .∴A1B1与平面A1ECF所成角的正切值为
.∴A1B1与平面A1ECF所成角的正切值为 .
.
探究创新
3.四面体的一条棱长是x,其他各条棱长为1.
(1)把四面体的体积V表示为x的函数f(x);
(2)求f(x)的值域;
(3)求f(x)的单调区间.
解:(1)设BC=x,则S到平面ABC的垂足O是△ABC的外心,连结AO并延长交BC于D,则D是BC的中点,且AD⊥BC,求得AD= ,S
,S =
=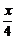
 .
.

设△ABC的外接圆的半径为R,求得R= ,SO=
,SO=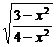 ,
,
∴V=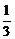 S
S ·SO=
·SO=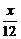
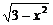 (0<x<
(0<x<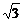 ).
).
(2)f(x)=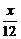
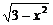 =
=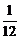
 =
=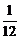
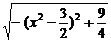 ,
,
∵0<x2<3,∴f(x)∈(0,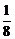 ).
).
(3)∵当x= 时,f(x)取得最大值,
时,f(x)取得最大值,
又∵0<x<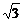 ,∴f(x)的单调递增区间是(0,
,∴f(x)的单调递增区间是(0, ],递减区间是[
],递减区间是[ ,
,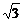 ).
).
2.如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为_____________.

答案: 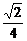
培养能力
1.每个顶点处棱都是3条的正多面体共有
A.2种 B.3种 C.4种 D.5种
解析:正多面体只有5种.
答案:B
3.在正方体ABCD-A1B1C1D1中,M、N分别是A1B1、BB1的中点,则直线AM与CN所成的角的余弦值是_____________.
解析:过N作NP∥AM交AB于点P,连结C1P,解三角形即可.
答案: 
●典例剖析
[例1] 已知甲烷CH4的分子结构是中心一个碳原子,外围有4个氢原子(这4个氢原子构成一个正四面体的四个顶点).设中心碳原子到外围4个氢原子连成的四条线段两两组成的角为θ,则cosθ等于
A.-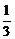 B.
B.
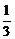 C.-
C.-
 D.
D.

解析:将正四面体嵌入正方体中,计算易得
cosθ= =-
=-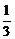 (设正方体的棱长为2).
(设正方体的棱长为2).
答案:A
[例2] 试求正八面体二面角的大小及其两条异面棱间的距离.
解:如图,设正八面体的棱长为4a,以中心O为原点,对角线DB、AC、QP为x轴、y
轴、z轴建立空间直角坐标系,则A(0,-2 a,0)、B(2
a,0)、B(2 a,0,0)、C(0,2
a,0,0)、C(0,2 a,0)、P(0,0,2
a,0)、P(0,0,2 a),设E为BC的中点,连结PE、QE、OE,则∠PEQ=2∠PEO即为所求二面角的平面角,∵OE=2a,OP=2
a),设E为BC的中点,连结PE、QE、OE,则∠PEQ=2∠PEO即为所求二面角的平面角,∵OE=2a,OP=2 a,∴tan∠PEO=
a,∴tan∠PEO= ,∠PEQ=2arctan
,∠PEQ=2arctan .设n=(x,y,z)是AB与PC的公垂线的一个方向向量,则有n·
.设n=(x,y,z)是AB与PC的公垂线的一个方向向量,则有n· =x+y=0,n·
=x+y=0,n· =y-z=0,解得
=y-z=0,解得
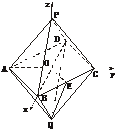
n=(-1,1,1),所以向量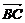 =(-2
=(-2 a,2
a,2 a,0)在n上的射影长d=
a,0)在n上的射影长d=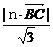 =
=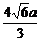 即为所求.
即为所求.
特别提示
由于正多面体中的等量关系、垂直关系比较多,所以便于建立直角坐标系,运用解析法处理.要注意恰当选取坐标原点,一般取其中心或顶点(如正四棱柱).
[例3] 三个12×12 cm的正方形,如图,都被连结相邻两边中点的直线分成A、B两片(如图(1)),把6片粘在一个正六边形的外面(如图(2)),然后折成多面体(如图(3)),求此多面体的体积.

解法一: 补成一个正方体,如图甲,V= V正方体=
V正方体= ×123=864 cm3.
×123=864 cm3.
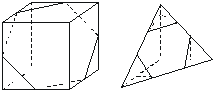
甲 乙
解法二:补成一个三棱锥,如图乙,V=V大三棱锥-3V小三棱锥=864 cm3.
思考讨论
补形的方法可将不规则的几何体转化成规则的几何体,这是求多面体体积的常用方法.
●闯关训练
夯实基础
2.正多面体只有_____________种,分别为________________.
答案:5 正四面体、正六面体、正八面体、正十二面体、正二十面体
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com