1.球的面积、体积及基本性质是解决有关问题的重要依据，它的轴截面图形、球半径、截面圆半径、圆心距所构成的直角三角形是把空间问题转化为平面问题的主要切入点.

9.在一个轴截面是正三角形的圆锥形容器中注入高为h的水，然后将一个铁球放入这个圆锥形的容器中，若水面恰好和球面相切，求这个铁球的半径.

解：如图，作出圆锥形容器的轴截面，△ABS为等边三角形.

∵SG=h，DG=h，∴V_水=·DG²·SG= h³.

设铁球的半径为R，

则SO=2R，SF=3R，

在Rt△FSB中 ，BF=SFtan∠FSB=R，

设放入球之后，球与水共占体积为V′，

则V′=·(BF)²·SF=(R)²·3R=3πR³，V_球= R³.

依题意，有V′=V_球+V_水，

即3πR³= R³+h³，∴R= h.

答：铁球的半径为h.

●思悟小结

8.(文)将半径为R的四个球，两两相切的放在桌面上，求上面一个球的球心与桌面的距离.

解：如下图，作OH⊥面O₁O₂O₃，

∵O₃H= R，

∴OH== 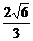R，球心与桌面的距离为( 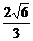+1)R.

(理)设A、B、C是半径为1的球面上的三点，B、C两点间的球面距离为，点A与B、C两点间的球面距离均为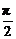，O为球心，求：

(1)∠AOB、∠BOC的大小；

(2)球心O到截面ABC的距离.

解：如图，(1)因为球O的半径为1，B、C两点间的球面距离为，点A与B、C两点间的球面距离均为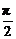，所以∠BOC=，∠AOB=∠AOC=.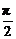

(2)因为BC=1，AC=AB=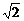，所以由余弦定理得cos∠BAC=，sin∠BAC=，设截面圆的圆心为O₁，连结AO₁，则截面圆的半径R=AO₁，由正弦定理得r== ，所以OO₁==.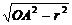

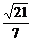探究创新

7.已知球面上的三点A、B、C，AB=6，BC=8，AC=10，球的半径为13，求球心到平面ABC的距离.

解：∵6²+8²=10²，∴△ABC为Rt△.

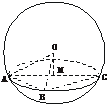
∵球心O在平面ABC内的射影M是截面圆的圆心，∴M是AC的中点且OM⊥AC.

在Rt△OAM中，OM==12.

∴球心到平面ABC的距离为12.

6.如图，三棱锥V-ABC中，VA⊥底面ABC，∠ABC=90°.

(1)求证：V、A、B、C四点在同一球面上；

(2)过球心作一平面与底面内直线AB垂直，求证：此平面截三棱锥所得的截面是矩形.

证明：(1)取VC的中点M，

∵VA⊥底面ABC，∠ABC=90°，∴BC⊥VB.在Rt△VBC中，M为斜边VC的中点，

∴MB=MC=MV.同理，在Rt△VAC中，MA=MV=MC.

∴MV=MC=MA=MB.

∴V、A、B、C四点在同一圆面上，M是球心.

(2)取AC、AB、VB的中点分别为N、P、Q，连结NP、PQ、QM、MN，则MNPQ就是垂直于AB的三棱锥V-ABC的截面，易证PQMN是平行四边形.又VA⊥BC，QP∥VA，NP∥BC，∴QP⊥PN.故截面MNPQ是矩形.

培养能力

5.把地球看作半径为R的球，A、B是北纬30°圈上的两点，它们的经度差为60°，求A、B两点间的球面距离.

解：如图，设30°纬度圈的圆心为O₁，半径为r，则r=Rcos30°.依题意∠AO₁B=60°，

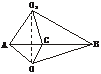
取AB的中点C，则BC=Rcos30°sin30°=R，

在Rt△BOC中，sin∠BOC=sin∠AOB==，

∴∠AOB=2arcsin，从而A、B两点的球面距离为2Rarcsin.

4.有两个半径都是r的球，其中一个球的球心在另一个球的球面上，则这两个球的交线长为_____________.

解析：由题意易得交线为半径为r的圆周，其长为πr.

答案：πr

3.已知球内接正方体的表面积为S，那么球的体积等于_____________.

解析：易知球直径2R等于正方体的对角线长a，由6a²=S，得a=，所以V_球=R³=

(a)³=(·)³=.

答案：

2.已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB=BC=CA=2，则球面面积是

A.　　　　　　　　　　　　 B.　　　　　　　　　　　　　 C.4π　　　　　　　　　　　　　 D.

解析：因为AB=BC=CA=2，所以△ABC的外接圆半径为r=.设球半径为R，则R²－(R)²=，所以R²=，S=4πR²=.

答案：D

1.(2004年全国Ⅱ，7)已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离均为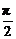，则球心O到平面ABC的距离为

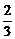A. 　　　　　　　　　　　　　 B. 　　　　　　　　　　　　 C. 　　　　　　　　　　　　　 D.

解析：显然OA、OB、OC两两垂直，如图，设O₁为ABC所在平面截球所得圆的圆心，

∵OA=OB=OC=1，且OA⊥OB⊥OC，

∴AB=BC=CA=.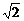

∴O₁为△ABC的中心.∴O₁A=.

由OO₁²+O₁A²=OA²，可得OO₁=.

答案：B