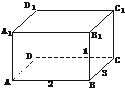
2.长方体AC₁的长、宽、高分别为3、2、1，从A到C₁沿长方体的表面的最短距离为

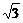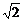A.1+　　　　　　　　　　　 B.2+　　　　　　　　　　 C.3　　　　　　　　　　　　 D.2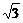

解析：求表面上最短距离常把图形展成平面图形.

答案：C

1.若Rt△ABC的斜边BC在平面α内，顶点A在α外，则△ABC在α上的射影是

A.锐角三角形　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.钝角三角形

C.直角三角形　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.一条线段或一钝角三角形

解析：当平面ABC⊥α时，为一条线段，结合选择肢，知选D.

答案：D

4.平面图形的翻折，空间向量的应用.

●点击双基

3.柱、锥、球的面积与体积.

2.空间角与空间距离.

1.线与线、线与面、面与面间的平行、垂直关系.

9.13　 立体几何的综合问题

●知识梳理

2.球是最常见的几何体.高考对球的考查主要在以下四个方面：(1)球的截面的性质；(2)球的表面积和体积；(3)球面上两点间的球面距离；(4)球与其他几何体的组合体.而且多以选择题和填空题的形式出现.第(4)方面有时用综合题进行考查.　　

拓展题例

[例1] 如图，一个广告气球被一束入射角为α的平行光线照射，其投影是一个长半轴为5 m的椭圆，则制作这个广告气球至少需要的面料是__________.

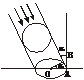
解析：长半轴为OA=5，∠AOB=α，设气球半径为r，则r=5cosα，

∴S=4πr²=100πcos²α m².

答案：100πcos²α m²

[例2] 三棱锥A-BCD的两条棱AB=CD=6，其余各棱长均为5，求三棱锥的内切球半径.

解法一：易知内切球球心O到各面的距离相等.

设E、F为CD、AB的中点，则O在EF上且O为EF的中点.

在△ABE中，AB=6，AE=BE=4，OH=.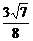

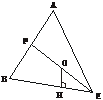
解法二：设球心O到各面的距离为R.

4×S×R=V_A-BCD，

∵S=×6×4=12，

V_A-BCD=2V_C-ABE=6.

∴4××12R=6.

∴R=.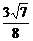

评述：正多面体与球的切接问题常借助体积求解.

1.要使学生理解两点的球面距离，掌握球的表面积及球的体积公式.求球面面积、球的体积及两点的球面距离是学习本节的重点.

2.要正确地区别球面上两点间的直线距离与球面距离.计算A、B两点间的球面距离的关键是搞清纬度、经度、纬度差、经度差等概念.

●教师下载中心

教学点睛