
7.(文)如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.

(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成的角.
(1)证明:以A为原点,AB、AD、AP所在直线为坐标轴,建立空间直角坐标系,则
A(0,0,0),B(a,0,0),D(0,2a,0),P(0,0,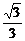 a),
a), ·
· =(a,0,0)·(0,2a,-
=(a,0,0)·(0,2a,-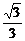 a)=0,又
a)=0,又 ·
· =0,
=0,
∴ ⊥
⊥ ,
, ⊥
⊥ .∴PD⊥BE.
.∴PD⊥BE.
(2)解:∵PA⊥面ABCD,PD与底面成30°角,∴∠PDA=30°.
过E作EF⊥AD,垂足为F,则AE=a,∠EAF=60°,AF=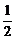 a,EF=
a,EF= a,
a,
∴E(0,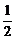 a,
a, a).
a).
于是 =(0,
=(0,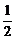 a,
a, a).又C(a,a,0),D(0,2a,0),∴CD=(-a,a,0).
a).又C(a,a,0),D(0,2a,0),∴CD=(-a,a,0).
cos〈 ,
, 〉=
〉=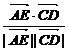 =
= =
= ,
,
∴异面直线AE与CD所成的角是arccos .
.
(理)四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,CD∥AB,AB=4,CD=1,点M在PB上,且MB=3PM,PB与平面ABC成30°角,
(1)求证:CM∥面PAD;
(2)求证:面PAB⊥面PAD;
(3)求点C到平面PAD的距离.
分析:本题主要考查空间直角坐标系的概念、空间点和向量的坐标表示以及用向量法证明平行关系,同时考查向量研究空间图形的数学思想方法.
如下图,建立空间直角坐标系O-xyz,C为坐标原点O,突破点在于求出相关的向量所对应的坐标.
(1)证明:如图,建立空间直角坐标系.

∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,即∠PBC=30°.
∵|PC|=2,∴|BC|=2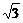 ,|PB|=4.
,|PB|=4.
得D(1,0,0)、B(0,2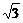 ,0)、A(4,2
,0)、A(4,2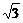 ,0)、P(0,0,2).
,0)、P(0,0,2).
∵|MB|=3|PM|,
∴|PM|=1,M(0, ,
, ),
),
 =(0,
=(0, ,
, ),
),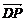 =(-1,0,2),
=(-1,0,2), =(3,2
=(3,2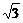 ,0).
,0).
设 =x
=x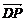 +y
+y (x、y∈R),
(x、y∈R),
则(0, ,
, )=x(-1,0,2)+y(3,2
)=x(-1,0,2)+y(3,2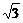 ,0)
,0) x=
x= 且y=
且y=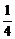 ,
,
∴ =
=

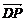 +
+ 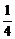
 .
.
∴ 、
、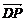 、
、 共面.又∵C
共面.又∵C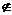 平面PAD,故CM∥平面PAD.
平面PAD,故CM∥平面PAD.
(2)证明:过B作BE⊥PA,E为垂足.
∵|PB|=|AB|=4,∴E为PA的中点.
∴E(2,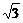 ,1),
,1), =(2,-
=(2,-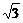 ,1).
,1).
又∵ ·
· =(2,-
=(2,-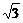 ,1)·(3,2
,1)·(3,2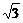 ,0)=0,
,0)=0,
∴ ⊥
⊥ ,即BE⊥DA.
,即BE⊥DA.
而BE⊥PA,∴BE⊥面PAD.
∵BE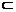 面PAB,∴面PAB⊥面PAD.
面PAB,∴面PAB⊥面PAD.
(3)解:由BE⊥面PAD知,平面PAD的单位向量n0= =
= (2,-
(2,-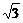 ,1).
,1).
∴CD=(1,0,0)的点C到平面PAD的距离
d=|n0· |=|
|=| (2,-
(2,-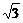 ,1)·(1,0,0)|=
,1)·(1,0,0)|= .
.
探究创新
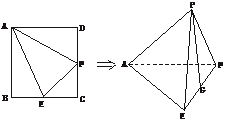
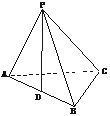
6.已知正方形ABCD的边长为1,分别取边BC、CD的中点E、F,连结AE、EF、AF,以AE、EF、FA为折痕,折叠使点B、C、D重合于一点P.
(1)求证:AP⊥EF;
(2)求证:平面APE⊥平面APF;
(3)求异面直线PA和EF的距离.
(1)证明:如下图,∵∠APE=∠APF=90°,PE∩PF=P,∴PA⊥平面PEF.
∵EF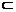 平面PEF,∴PA⊥EF.
平面PEF,∴PA⊥EF.
(2)证明:∵∠APE=∠EPF=90°,AP∩PF=P,∴PE⊥平面APF.又PE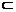 平面PAE,∴平面APE⊥平面APF.
平面PAE,∴平面APE⊥平面APF.
(3)解:在面PEF中,作PG⊥EF,垂足为G,∵AP与面PEF垂直,PG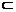 平面PEF,
平面PEF,
∴AP⊥PG,PG⊥EF,PG是AP与EF的公垂线.在等腰Rt△PEF中,PE=PF=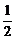 ,∠EPF=90°,∴PG=EG=
,∠EPF=90°,∴PG=EG=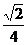 .
.
5.把长、宽各为4、3的长方形ABCD,沿对角线AC折成直二面角,求顶点B和顶点D的距离.
解:如图,作BE⊥AC于E,

∵二面角B-AC-D为直二面角,BE⊥AC,
∴BE⊥平面ADC,DE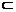 平面ADC,BE⊥DE.
平面ADC,BE⊥DE.
在Rt△ABC中,可得BE= ,AE=
,AE=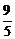 ,在△ADE中,DE2=AE2+AD2-2AD·AE·
,在△ADE中,DE2=AE2+AD2-2AD·AE·
cos∠EAD=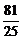 +16-2·
+16-2·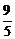 ·4·
·4· =
= .
.
在Rt△BDE中,BD=BE2+ED2= .
.
培养能力
4.在三棱锥P-ABC中,底面是边长为2 cm的正三角形,PA=PB=3 cm,转动点P时,三棱锥的最大体积为.
解析:点P到面ABC距离最大时体积最大,此时面PAB⊥面ABC,高PD=2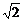 .
.
V=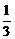 ×
× ×4×2
×4×2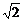 =
=  .
.
答案: cm3
cm3
3.图甲是一个正三棱柱形的容器,高为2a,内装水若干.现将容器放倒,把一个侧面作为底面,如图乙所示,这时水面恰好为中截面,则图甲中水面的高度为_____________.

解析:设正三棱柱的底面积为S,将图乙竖起得图丙,则V水=V柱-V =S·2a-(
=S·2a-(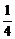 S)·2a=
S)·2a= aS.设图甲中水面的高度为x,则S·x=
aS.设图甲中水面的高度为x,则S·x= aS,得x=
aS,得x= a.
a.
答案:
2.在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为

A.arccos B.arccos
B.arccos C.arccos
C.arccos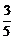 D.arccos
D.arccos
解法一:∵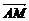 =
= +
+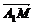 ,
, =
= 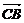 +
+ ,
,
∴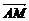 ·
· =(
=( +
+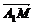 )·(
)·(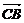 +
+ )=
)= ·
· =
= 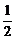 .
.
而|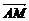 |=
|=  =
=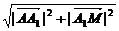 =
= 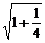 =
= 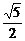 .同理,|
.同理,| |=
|=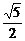 .
.
如令α为所求之角,则cosα=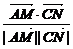 =
= =
= ,∴α=arccos
,∴α=arccos .应选D.
.应选D.
解法二:建立如图所示的空间直角坐标系,把D点视作原点O,分别以 、
、 、
、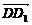 的方向为x轴、y轴、z轴的正方向,则A(1,0,0)、M(1,
的方向为x轴、y轴、z轴的正方向,则A(1,0,0)、M(1,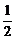 ,1)、C(0,1,0)、N(1,1,
,1)、C(0,1,0)、N(1,1,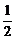 ).
).

∴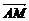 =(0,
=(0,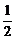 ,1),
,1), =(1,0,
=(1,0,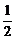 ).
).
故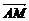 ·
· =0×1+
=0×1+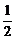 ×0+1×
×0+1×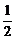 =
=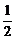 ,
,
|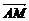 |=
|= =
=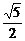 ,
,
| |=
|= =
=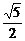 .
.
∴cosα=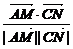 =
= =
= .
.
∴α=arccos .
.
答案:D
1.下图是一个无盖的正方体盒子展开后的平面图,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的值为

A.180° B.120° C.60° D.45°
答案:C
4.棱长为a的正方体的各个顶点都在一个球面上,则这个球的体积是_____________.
解析:易知球的直径2R=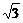 a.所以R=
a.所以R= a.所以V=
a.所以V=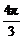 R3=
R3= a3.
a3.
答案: a3
a3
3.设长方体的对角线长为4,过每个顶点的三条棱中总有两条棱与对角线的夹角为60°,则长方体的体积是
A.27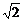 B.8
B.8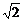 C.8
C.8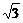 D.16
D.16
解析:先求出长方体的两条棱长为2、2,设第三条棱长为x,由22+22+x2=42 x=2
x=2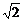 ,∴V=2×2×2
,∴V=2×2×2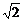 =8
=8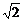 .
.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com