2.(2004年北京，3)设m、n是两条不同的直线，α、β、γ是三个不同的平面.给出下列四个命题，其中正确命题的序号是

①若m⊥α，n∥α，则m⊥n　 ②若α∥β，β∥γ，m⊥α，则m⊥γ　 ③若m∥α，n∥α，则m∥n　 ④若α⊥γ，β⊥γ，则α∥β

A.①②　　　　　　　　　　　　 B.②③　　　　　　　　　　　　 C.③④　　　　　　　　　　　　 D.①④

解析：①②显然正确.③中m与n可能相交或异面.④考虑长方体的顶点，α与β可以相交.

答案：A

1.设有平面α、β和直线m、n，则m∥α的一个充分条件是

A.α⊥β且m⊥β　　 B.α∩β=n且m∥n　　 C.m∥n且n∥α　　　　　 D.α∥β且m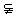β

答案：D

3.直线与平面平行的性质：如果一条直线与一个平面平行，经过这条直线的平面与已知平面相交，那么这条直线与交线平行.

●点击双基

2.直线与平面平行的判定：如果平面外的一条直线与平面内的一条直线平行，那么这条直线与这个平面平行.

1.直线与平面的位置关系有且只有三种，即直线与平面平行、直线与平面相交、直线在平面内.

9.2　 直线与平面平行

●知识梳理

3.在综合问题中，首先要注意是否构建直角坐标系，能较易建立直角坐标系的，尽量建立直角坐标系.其次要注意向量运算与基本性质相结合的论述，这是今后的方向，可以“形到形”，可以“数到形”，注意数形结合，向量方法与传统方法各有千秋，相得益彰.

必须熟练掌握向量的基本知识和技能，尤其提出如下几点：

(1)怎样选择应用基底(不设直角坐标系)和建立直角坐标系及坐标系建立技巧；

(2)法向量的应用对处理角和距离的重要性；

(3)怎样用向量解决立体几何中的几大常见题型；

(4)准确判断是否选用向量处理问题，明确向量解题的缺点；

(5)空间向量是怎样由平面向量拓展而来的.

●教师下载中心

教学点睛

要给学生归纳、总结，使学生系统地掌握线线、线面、面面的位置关系，特别是平行与垂直的判定与性质，通过对照，深刻理解异面直线所成的角、斜线与平面所成的角、二面角的平面角，理解点到面的距离、异面直线的距离.通过解题总结证明立体几何问题的常见方法，注意培养学生的空间想象能力.

拓展题例

[例1] 已知直线a∥α，且a与α间的距离为d，a在α内的射影为a′，l为平面α内与a′平行的任一直线，则a与l之间的距离的取值范围是

A.［d，+∞)　　　　 B.(d，+∞)　　　　　　　 C.(0，d］　　　　　　　　　 D.{d}

解析：如图，在a上任取一点P作PO⊥a′，垂足为O，过O作OA⊥l，垂足为A，连结PA.则PA⊥l，PA⊥a，故PA就是a与l之间的距离.在Rt△POA中，PA>PO=d，选B.

答案：B

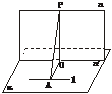
[例2] 如图，已知底面半径为r的圆柱被一个平面所截，剩下部分母线长的最大值为a，最小值为b，那么圆柱被截后剩下部分的体积是__________.

解析：两个相同的几何体

倒立一个，对应合缝，恰好形成一个圆柱体.

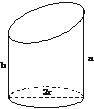
答案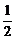：πr²(a+b)

[例3] (2003年北京西城区一模题)如图，正三棱柱ABC-A₁B₁C₁的所有棱长均为2，P是侧棱AA₁上任意一点.

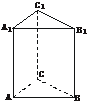
(1)求证：B₁P不可能与平面ACC₁A₁垂直；　 (2)当BC₁⊥B₁P时，求线段AP的长；(3)在(2)的条件下，求二面角C-B₁P-C₁的大小.

(1)证明：连结B₁P，假设B₁P⊥平面ACC₁A₁，则B₁P⊥A₁C₁.

由于三棱柱ABC-A₁B₁C₁为正三棱柱，

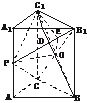
∴AA₁⊥A₁C₁.

∴A₁C₁⊥侧面ABB₁A₁.

∴A₁C₁⊥A₁B₁，

即∠B₁A₁C₁=90°.

这与△A₁B₁C₁是等边三角形矛盾.

∴B₁P不可能与平面ACC₁A₁垂直.

(2)解：取A₁B₁的中点D，连结C₁D、BD、BC₁，

则C₁D⊥A₁B₁，又∵AA₁⊥平面A₁B₁C₁，

∴AA₁⊥C₁D.∴C₁D⊥平面ABB₁A₁.

∴BD是BC₁在平面ABB₁A₁上的射影.

∵BC₁⊥B₁P，∴BD⊥B₁P.∴∠B₁BD=90°－∠BB₁P=∠A₁B₁P.

又A₁B₁=B₁B=2，∴△BB₁D≌△B₁A₁P，A₁P=B₁D=1.∴AP=1.

(3)解：连结B₁C，交BC₁于点O，则BC₁⊥B₁C.又BC₁⊥B₁P，∴BC₁⊥平面B₁CP.

过O在平面CPB₁上作OE⊥B₁P，交B₁P于点E，连结C₁E，则B₁P⊥C₁E，

∴∠OEC₁是二面角C-B₁P-C₁的平面角.

由于CP=B₁P=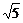，O为B₁C的中点，连结OP，

∴PO⊥B₁C，OP·OB₁=OE·B₁P.∴OE=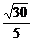.∴tan∠OEC₁==.

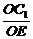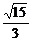∴∠OEC₁=arctan.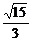

故二面角C-B₁P-C₁的大小为arctan.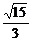

2.线线垂直、两异面直线的夹角、两点间的距离等问题的解决往往借助于向量坐标.正方体、长方体、底面有一角为直角的直棱柱、底面为菱形的直四棱柱、四棱锥等凡能出现三条两两垂直直线的图形，常常考虑空间直角坐标系.

1.利用向量解立体几何问题，要仔细分析问题特点，把已知条件用向量表示，把一些待求的量用基向量或其他向量表示，将几何的位置关系的证明问题或数量关系的运算问题转化为典型的向量运算，以算代证，以值定形.这种方法可减少复杂的空间结构分析，使得思路简捷、方法清晰、运算直接，能迅速准确地解决问题.

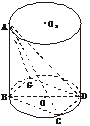
8.(2003年北京宣武区二模题)如图，AB为圆柱OO₁的母线，BD为圆柱OO₁下底面直径，AB=BD=2，点C为下底面圆周⊙O上的一点，CD=1.

(1)求三棱锥C-ABD的体积；

(2)求面BAD与面CAD所成二面角的大小；

(3)求BC与AD所成角的大小.

分析：本题主要考查直线、平面的位置关系，考查圆柱的有关概念，考查直线、平面所成角的概念及求法，考查空间想象能力和推理能力.

解：(1)∵AB为圆柱OO₁的母线，∴AB⊥下底面.

∴AB为棱锥A-BCD的高.而点C在⊙O上，∴△BCD为直角三角形，∠BCD=90°.

∵BD=2，CD=1，∴BC=.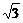

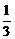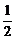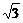∴V_{三棱锥C-ABD}=V_{三棱锥A-BCD}=××1××2=.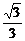

(2)过B作BE⊥AD，垂足为E，过点B作BF⊥AC，垂足为点F，连结EF.由BD为底面圆的直径，得BC⊥CD.

∵AB⊥平面BCD，BC⊥CD，

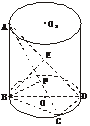
∴AC⊥CD.

而AC∩BC=C，

∴CD⊥平面ABC.

而CD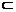平面ADC，

∴平面ABC⊥平面ADC，且它们的交线为AC.

∵BF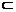平面ABC，BF⊥AC，垂足为点F，

∴BF⊥平面ACD.

而BE⊥AD，AD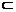平面ACD，

∴EF⊥AD.平面ABD∩平面ACD=AD，

∴∠BEF是面ABD与面ACD所成的二面角的平面角.

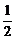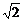由BE=AD=，AC=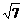，AB=2，可求出BF=.

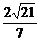∴sin∠BEF===.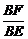

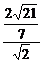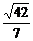∵∠BEF为锐角，∴∠BEF=arcsin.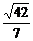

故所求二面角的大小为arcsin.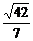

(3)过点D在下底面作DG∥BC交⊙O于点G，则∠GDA为BC与AD所成的角.连结BG、AG，由BD是⊙O的直径，得GD⊥BG，则AG⊥DG，BC=GD.

∴cos∠GDA===.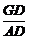

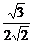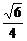∴∠GDA=arccos.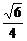

∴所求BC与AD所成的角的大小为arccos.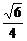

●思悟小结