
7.已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线,(1)求证:D1B1∥l;(2)若AB=a,求l与D1间的距离.

(1)证明:

∵D1B1∥BD,
∴D1B1∥平面ABCD.
又平面ABCD∩平面AD1B1=l,
∴D1B1∥l.
(2)解:∵D1D⊥平面ABCD,
在平面ABCD内,由D作DG⊥l于G,连结D1G,则D1G⊥l,D1G的长即等于点D1与l间的距离.
∵l∥D1B1∥BD,∴∠DAG=45°.
∴DG= a,D1G=
a,D1G= =
=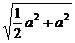 =
= a.
a.
探究创新
6.如下图,设P为长方形ABCD所在平面外一点,M、N分别为AB、PD上的点,且 =
= ,求证:直线MN∥平面PBC.
,求证:直线MN∥平面PBC.

分析:要证直线MN∥平面PBC,只需证明MN∥平面PBC内的一条直线或MN所在的某个平面∥平面PBC.
证法一:过N作NR∥DC交PC于点R,连结RB,依题意得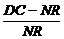 =
= =
= =
=
 =
=
 NR=MB.∵NR∥DC∥AB,∴四边形MNRB是平行四边形.∴MN∥RB.又∵RB
NR=MB.∵NR∥DC∥AB,∴四边形MNRB是平行四边形.∴MN∥RB.又∵RB 平面PBC,∴直线MN∥平面PBC.
平面PBC,∴直线MN∥平面PBC.
证法二:过N作NQ∥AD交PA于点Q,连结QM,∵ =
= =
= ,∴QM∥PB.又NQ∥AD∥BC,∴平面MQN∥平面PBC.∴直线MN∥平面PBC.
,∴QM∥PB.又NQ∥AD∥BC,∴平面MQN∥平面PBC.∴直线MN∥平面PBC.
证法三:过N作NR∥DC交PC于点R,连结RB,依题意有 =
= =
= ,∴
,∴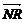 =
= ,
,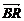 =
= +
+ +
+ 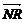 =
= .∴MN∥RB.又∵RB
.∴MN∥RB.又∵RB 平面PBC,∴直线MN∥平面PBC.
平面PBC,∴直线MN∥平面PBC.
培养能力
5.如下图,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= a,试在AB上找一点F,使EF∥平面PAD.
a,试在AB上找一点F,使EF∥平面PAD.

解:在面PCD内作EG⊥PD于G,连结AG.
∵PA⊥平面ABCD,CD⊥AD,
∴CD⊥PD.∴CD∥EG.
又AB∥CD,∴EG∥AB.
若有EF∥平面PAD,则EF∥AG,
∴四边形AFEG为平行四边形,得EG=AF.
∵CE= =
=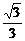 a,△PBC为直角三角形,∴BC2=CE·CP
a,△PBC为直角三角形,∴BC2=CE·CP CP=
CP= a,
a,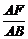 =
=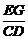 =
=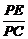 =
= =
= .
.
故得AF∶FB=2∶1时,EF∥平面PAD.
4.已知Rt△ABC的直角顶点C在平面α内,斜边AB∥α,AB=2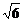 ,AC、BC分别和平面α成45°和30°角,则AB到平面α的距离为__________.
,AC、BC分别和平面α成45°和30°角,则AB到平面α的距离为__________.
解析:分别过A、B向平面α引垂线AA′、BB′,垂足分别为A′、B′.

设AA′=BB′=x,
则AC2=( )2=2x2,
)2=2x2,
BC2=( )2=4x2.
)2=4x2.
又AC2+BC2=AB2,∴6x2=(2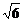 )2,x=2.
)2,x=2.
答案:2
3.(2004年全国Ⅰ,16)已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.
在上面结论中,正确结论的编号是__________.(写出所有正确结论的编号)
解析:A1D与BC1在平面ABCD上的射影互相平行;
AB1与BC1在平面ABCD上的射影互相垂直;
DD1与BC1在平面ABCD上的射影是一条直线及其外一点.

答案:①②④
2.a、b是两条异面直线,A是不在a、b上的点,则下列结论成立的是
A.过A有且只有一个平面平行于a、b B.过A至少有一个平面平行于a、b
C.过A有无数个平面平行于a、b D.过A且平行a、b的平面可能不存在
解析:过点A可作直线a′∥a,b′∥b,
则a′∩b′=A.
∴a′、b′可确定一个平面,记为α.
如果a α,b
α,b α,则a∥α,b∥α.
α,则a∥α,b∥α.
由于平面α可能过直线a、b之一,因此,过A且平行于a、b的平面可能不存在.
答案:D
1.两条直线a、b满足a∥b,b α,则a与平面α的关系是
α,则a与平面α的关系是
A.a∥α
B.a与α相交 C.a与α不相交 D.a α
α
答案:C
5.在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是________.

解析:连结AM并延长,交CD于E,连结BN并延长交CD于F,由重心性质可知,E、F重合为一点,且该点为CD的中点E,由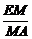 =
= =
= 得MN∥AB,
得MN∥AB,
因此,MN∥平面ABC且MN∥平面ABD.
答案:平面ABC、平面ABD
●典例剖析
[例1] 如下图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.

证法一:过M作MP⊥BC,NQ⊥BE,P、Q为垂足(如上图),连结PQ.
∵MP∥AB,NQ∥AB,∴MP∥NQ.
又NQ= BN=
BN= CM=MP,∴MPQN是平行四边形.
CM=MP,∴MPQN是平行四边形.
∴MN∥PQ,PQ 平面BCE.
平面BCE.
而MN 平面BCE,
平面BCE,
∴MN∥平面BCE.
证法二:过M作MG∥BC,交AB于点G(如下图),连结NG.

∵MG∥BC,BC 平面BCE,
平面BCE,
MG 平面BCE,
平面BCE,
∴MG∥平面BCE.
又 =
= =
=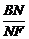 ,
,
∴GN∥AF∥BE,同样可证明GN∥平面BCE.
又面MG∩NG=G,
∴平面MNG∥平面BCE.又MN 平面MNG.∴MN∥平面BCE.
平面MNG.∴MN∥平面BCE.
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行.
[例2] 如下图,正方体ABCD-A1B1C1D1中,侧面对角线AB1、BC1上分别有两点E、F,且B1E=C1F.求证:EF∥平面ABCD.

证法一:分别过E、F作EM⊥AB于点M,FN⊥BC于点N,连结MN.
∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC.
∴EM∥BB1,FN∥BB1.∴EM∥FN.
又B1E=C1F,∴EM=FN.
故四边形MNFE是平行四边形.
∴EF∥MN.又MN在平面ABCD中,
∴EF∥平面ABCD.
证法二:过E作EG∥AB交BB1于点G,连结GF,则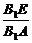 =
= .
.
∵B1E=C1F,B1A=C1B,∴ =
= .
.
∴FG∥B1C1∥BC.
又∵EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD.而EF在平面EFG中,
∴EF∥平面ABCD.
评述:证明线面平行的常用方法是:证明直线平行于平面内的一条直线;证明直线所在的平面与已知平面平行.
[例3] 已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM∶MA=BN∶ND=5∶8.

(1)求证:直线MN∥平面PBC;
(2)求直线MN与平面ABCD所成的角.
(1)证明:∵P-ABCD是正四棱锥,∴ABCD是正方形.连结AN并延长交BC于点E,连结PE.
∵AD∥BC,∴EN∶AN=BN∶ND.
又∵BN∶ND=PM∶MA,
∴EN∶AN=PM∶MA.
∴MN∥PE.
又∵PE在平面PBC内,∴MN∥平面PBC.
(2)解:由(1)知MN∥PE,∴MN与平面ABCD所成的角就是PE与平面ABCD所成的角.
设点P在底面ABCD上的射影为O,连结OE,则∠PEO为PE与平面ABCD所成的角.
由正棱锥的性质知PO= =
=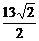 .
.
由(1)知,BE∶AD=BN∶ND=5∶8,
∴BE= .
.
在△PEB中,∠PBE=60°,PB=13,BE= ,
,
根据余弦定理,得PE= .
.
在Rt△POE中,PO=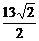 ,PE=
,PE= ,
,
∴sin∠PEO= =
= .
.
故MN与平面ABCD所成的角为arcsin .
.
思考讨论
证线面平行,一般是转化为证线线平行.求直线与平面所成的角一般用构造法,作出线与面所成的角.本题若直接求MN与平面ABCD所成的角,计算困难,而平移转化为PE与平面ABCD所成的角则计算容易.可见平移是求线线角、线面角的重要方法.
●闯关训练
夯实基础
4.(文)设平面α∥平面β,A、C∈α,B、D∈β,直线AB与CD交于点S,且AS=8,BS=9,CD=34,①当S在α、β之间时,SC=_____________,②当S不在α、β之间时,SC=_____________.
解析:∵AC∥BD,∴△SAC∽△SBD,①SC=16,②SC=272.
答案:①16 ②272
(理)设D是线段BC上的点,BC∥平面α,从平面α外一定点A(A与BC分居平面两侧)作AB、AD、AC分别交平面α于E、F、G三点,BC=a,AD=b,DF=c,则EG=_____________.
解析:解法类同于上题.
答案:
3.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是
A.异面 B.相交 C.平行 D.不能确定
解析:设α∩β=l,a∥α,a∥β,
过直线a作与α、β都相交的平面γ,
记α∩γ=b,β∩γ=c,
则a∥b且a∥c,
∴b∥c.
又b α,α∩β=l,∴b∥l.∴a∥l.
α,α∩β=l,∴b∥l.∴a∥l.

答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com