1.“直线l垂直于平面α内的无数条直线”是“l⊥α”的

A.充分条件　　　　　　　　　　　　　　　　　　　　　　　　　　 B.必要条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分又不必要条件

答案：B

3.直线与平面垂直的性质：如果两条直线都与同一个平面垂直，那么这两条直线平行.

●点击双基

2.直线与平面垂直的判定：如果一条直线与平面内的两条相交直线都垂直，那么这条直线与这个平面垂直.

1.如果一条直线与平面相交并且与平面内的所有直线都垂直，那么就说这条直线与这个平面垂直.

9.3　 直线与平面垂直

●知识梳理

2.证明线面平行是高考中常见的问题，常用的方法就是证明这条线与平面内的某条直线平行.

拓展题例

[例1] 如下图，设a、b是异面直线，AB是a、b的公垂线，过AB的中点O作平面α与a、b分别平行，M、N分别是a、b上的任意两点，MN与α交于点P，求证：P是MN的中点.

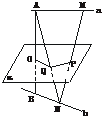
证明：连结AN，交平面α于点Q，连结PQ.

∵b∥α，b平面ABN，平面ABN∩α=OQ，

∴b∥OQ.又O为AB的中点，

∴Q为AN的中点.　　 ∵a∥α，a平面AMN且平面AMN∩α=PQ，

∴a∥PQ.∴P为MN的中点.

评述：本题重点考查直线与平面平行的性质.

[例2] 在直三棱柱ABC-A₁B₁C₁中，AB₁⊥BC₁，AB=CC₁=a，BC=b.

(1)设E、F分别为AB₁、BC₁的中点，求证：EF∥平面ABC；

(2)求证：A₁C₁⊥AB；

(3)求点B₁到平面ABC₁的距离.

(1)证明：∵E、F分别为AB₁、BC₁的中点，

∴EF∥A₁C₁.∵A₁C₁∥AC，∴EF∥AC.

∴EF∥平面ABC.

(2)证明：∵AB=CC₁，∴AB=BB₁.又三棱柱为直三棱柱，∴四边形ABB₁A₁为正方形.连结A₁B，则A₁B⊥AB₁.

又∵AB₁⊥BC₁，∴AB₁⊥平面A₁BC₁.

∴AB₁⊥A₁C₁.

又A₁C₁⊥AA₁，∴A₁C₁⊥平面A₁ABB₁.

∴A₁C₁⊥AB.

(3)解：∵A₁B₁∥AB，∴A₁B₁∥平面ABC₁.

∴A₁到平面ABC₁的距离等于B₁到平面ABC₁的距离.

过A₁作A₁G⊥AC₁于点G，

∵AB⊥平面ACC₁A₁，

∴AB⊥A₁G.从而A₁G⊥平面ABC₁，故A₁G即为所求的距离，即A₁G= .

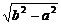评述：本题(3)也可用等体积变换法求解.　　

1.必须使学生理解并掌握直线与平面的位置关系，以及直线与平面平行的判定定理及性质定理；结合本课时题目，使学生掌握解证线面平行的基本方法.

2.辅助线(面)是解证线面平行的关键.为了能利用线面平行的判定定理及性质定理，往往需要作辅助线(面).

●教师下载中心

教学点睛

1.直线与平面的位置关系有三种：直线在平面内、直线与平面相交、直线与平面平行，后者又统称为直线在平面外.

8.如下图，在正四棱柱ABCD-A₁B₁C₁D₁中，AA₁=AB，点E、M分别为A₁B、C₁C的中点，过点A₁、B、M三点的平面A₁BMN交C₁D₁于点N.

(1)求证：EM∥平面A₁B₁C₁D₁；

(2)求二面角B-A₁N-B₁的正切值；

(3)设截面A₁BMN把该正四棱柱截成的两个几何体的体积分别为V₁、V₂(V₁＜V₂)，求V₁∶V₂的值.

(1)证明：设A₁B₁的中点为F，连结EF、FC₁.

∵E为A₁B的中点，∴EF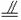B₁B.

又C₁M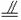B₁B，∴EF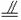MC₁.

∴四边形EMC₁F为平行四边形.

∴EM∥FC₁.∵EM平面A₁B₁C₁D₁，

FC₁平面A₁B₁C₁D₁，

∴EM∥平面A₁B₁C₁D₁.

(2)解：作B₁H⊥A₁N于H，连结BH.

∵BB₁⊥平面A₁B₁C₁D₁，∴BH⊥A₁N.

∴∠BHB₁为二面角B-A₁N-B₁的平面角.

∵EM∥平面A₁B₁C₁D₁，EM平面A₁BMN，平面A₁BMN∩平面A₁B₁C₁D₁=A₁N，

∴EM∥A₁N.

又∵EM∥FC₁，∴A₁N∥FC₁.

又∵A₁F∥NC₁，∴四边形A₁FC₁N是平行四边形.∴NC₁=A₁F.

设AA₁=a，则A₁B₁=2a，D₁N=a.

在Rt△A₁D₁N中，

A₁N== a，

∴sin∠A₁ND₁==.

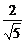在Rt△A₁B₁H中，B₁H=A₁B₁sin∠HA₁B₁=2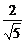a·= a.

在Rt△BB₁H中，

tan∠BHB₁===.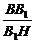

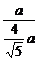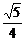(3)解：延长A₁N与B₁C₁交于P，则P∈平面A₁BMN，且P∈平面BB₁C₁C.

又∵平面A₁BMN∩平面BB₁C₁C=BM，

∴P∈BM，即直线A₁N、B₁C₁、BM交于一点P.

又∵平面MNC₁∥平面BA₁B₁，

∴几何体MNC₁-BA₁B₁为棱台.(没有以上这段证明，不扣分)

∵S=·2a·a=a²，

S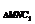=·a·a= a²，

棱台MNC₁-BA₁B₁的高为B₁C₁=2a，

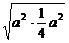V₁=·2a·(a²++a²)=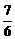 a³，∴V₂=2a·2a·a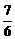－a³= a³.

∴=.

●思悟小结