
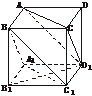
5.如下图,在正方体ABCD-A1B1C1D1中,AB=a.

(1)求证:平面AD1B1∥平面C1DB;
(2)求证:A1C⊥平面AD1B1;
(3)求平面AB1D1与平面BC1D之间的距离.
(1)证明:∵D1B1∥DB,∴D1B1∥平面C1DB.
同理,AB1∥平面C1DB.
又D1B1∩AB1=B1,
∴平面AD1B1∥平面C1DB.
(2)证明:∵A1C1⊥D1B1,而A1C1为A1C在平面A1B1C1D1上的射影,∴A1C1⊥D1B1.
同理,A1C⊥AB1,D1B1∩AB1=B1.
∴A1C⊥平面AD1B1.
(3)解:设A1C∩平面AB1D1=M,
A1C∩平面BC1D=N,O1、O分别为上底面A1B1C1D1、下底面ABCD的中心.
则M∈AO1,N∈C1O,且AO1∥C1O,
MN的长等于平面AD1B1与平面C1DB的距离,即MN=A1M=NC= A1C=
A1C=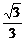 a.
a.
培养能力
4.如下图,两条线段AB、CD所在的直线是异面直线,CD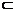 平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.

(1)求证:MN∥α;
(2)若AB=CD=a,AC=b,BD=c,求线段MN的长.
(1)证明:过B作BB′⊥α,垂足为B′,连结CB′、DB′,设E为B′D的中点,
连结NE、CE,则NE∥BB′且NE=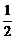 BB′,又AC=BB′,
BB′,又AC=BB′,
∴MC NE,即四边形MCEN为平行四边形(矩形).
NE,即四边形MCEN为平行四边形(矩形).
∴MN∥CE.又CE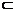 α,MN
α,MN α,∴MN∥α.
α,∴MN∥α.
(2)解:由(1)知MN=CE,AB=CB′=a=CD,B′D= =
= ,
,
∴CE= =
= ,
,
即线段MN的长为 .
.
3.如图甲,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题:

①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当容器倾斜如图乙时,EF·BF是定值.
其中正确命题的序号是_____________.
解析:对于命题①,由于BC固定,所以在倾斜的过程中,始终有AD∥EH∥FG∥BC,且平面AEFB∥平面DHGC,故水的部分始终呈棱柱状(四棱柱或三棱柱、五棱柱),且BC为棱柱的一条侧棱,命题①正确.对于命题②,当水是四棱柱或五棱柱时,水面面积与上下底面面积相等;当水是三棱柱时,则水面面积可能变大,也可能变小,故②不正确.③是正确的(请给出证明).④是正确的,由水的体积的不变性可证得.综上所述,正确命题的序号是①③④.
答案:①③④
2.设平面α∥β,A、C∈α,B、D∈β,直线AB与CD交于S,若AS=18,BS=9,CD=34,则CS=_____________.
解析:如图(1),由α∥β可知BD∥AC,
∴ =
=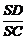 ,即
,即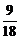 =
= ,∴SC=68.
,∴SC=68.

如图(2),由α∥β知AC∥BD,
∴ =
= =
=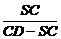 ,即
,即 =
= .
.
∴SC= .
.
答案:68或
1.(2003年上海)在下列条件中,可判断平面α与β平行的是
A.α、β都垂直于平面γ
B.α内存在不共线的三点到β的距离相等
C.l、m是α内两条直线,且l∥β,m∥β
D.l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
答案:D
4.a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,直线均不在平面内,给出六个命题:

其中正确的命题是________________.(将正确的序号都填上)
答案:①④⑤⑥
●典例剖析
[例1] 设平面α∥平面β,AB、CD是两条异面直线,M、N分别是AB、CD的中点,且A、C∈α,B、D∈β,求证:MN∥平面α.

剖析:因为AB与CD是异面直线,故MN与AC、BD不平行.在平面α、β中不易找到与MN平行的直线,所以试图通过证线线平行达到线面平行这一思路受阻,于是转而考虑通过证面面平行达到线面平行,即需找一个过MN且与α平行的平面.根据M、N是异面直线上的中点这一特征,连结BC,则此时AB、BC共面,即BC为沟通AB、CD的桥梁,再取BC的中点E,连结ME、NE,用中位线知识可证得.
证明:连结BC、AD,取BC的中点E,连结ME、NE,则ME是△BAC的中位线,故ME∥AC,ME α,∴ME∥α.同理可证,NE∥BD.又α∥β,设CB与DC确定的平面BCD与平面α交于直线CF,则CF∥BD,∴NE∥CF.而NE
α,∴ME∥α.同理可证,NE∥BD.又α∥β,设CB与DC确定的平面BCD与平面α交于直线CF,则CF∥BD,∴NE∥CF.而NE 平面α,CF
平面α,CF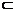 α,∴NE∥α.又ME∩
α,∴NE∥α.又ME∩
NE=E,∴平面MNE∥α,而MN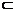 平面MNE,∴MN∥平面α.
平面MNE,∴MN∥平面α.
[例2] 如下图,在空间六边形(即六个顶点没有任何五点共面)ABCC1D1A1中,每相邻的两边互相垂直,边长均等于a,并且AA1∥CC1.求证:平面A1BC1∥平面ACD1.
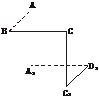
证法一:作正方形BCC1B1和CC1D1D,并连结A1B1和AD.
∵AA1 CC1
CC1 BB1
BB1 DD1,且AA1⊥AB,AA1⊥A1D1,
DD1,且AA1⊥AB,AA1⊥A1D1,
∴ABB1A1和AA1D1D都是正方形,且ACC1A1是平行四边形.
故它们的对应边平行且相等.
∵△ABC≌△A1B1C1,∴A1B1⊥B1C1.
同理,AD⊥CD.
∵BB1⊥AB,BB1⊥BC,∴BB1⊥平面ABC.
同理,DD1⊥平面ACD.
∵BB1∥DD1,∴BB1⊥平面ACD.
∴A、B、C、D四点共面.
∴ABCD为正方形.
同理,A1B1C1D1也是正方形.
故ABCD-A1B1C1D1是正方体.
易知A1C1∥AC,
∴A1C1∥平面ACD1.
同理,BC1∥平面ACD1,
∴平面A1BC1∥平面ACD1.
证法二:证ABCD-A1B1C1D1是正方体,同上.
连结B1D、B1D1,则B1D1是B1D在底面ABCD上的射影,
由三垂线定理知B1D⊥A1C1,
同理可证B1D⊥BA1,
∴B1D⊥平面A1BC1.
同理可证,B1D⊥平面ACD1,
∴平面A1BC1∥平面ACD1.
思考讨论
证明面面平行的常用方法:利用面面平行的判定定理;证明两个平面垂直于同一条直线.
[例3] 如下图,在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:
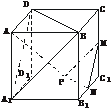
(1)AP⊥MN;
(2)平面MNP∥平面A1BD.
证明:(1)连结BC1、B1C,则B1C⊥BC1,BC1是AP在面BB1C1C上的射影.∴AP⊥B1C.
又B1C∥MN,∴AP⊥MN.
(2)连结B1D1,∵P、N分别是D1C1、B1C1的中点,
∴PN∥B1D1.又B1D1∥BD,
∴PN∥BD.又PN不在平面A1BD上,
∴PN∥平面A1BD.
同理,MN∥平面A1BD.又PN∩MN=N,
∴平面PMN∥平面A1BD.
评述:将空间问题转化为平面问题,是解决立体几何问题的重要策略,关键在于选择或添加适当的平面或线.由于M、N、P都为中点,故添加B1C、BC1作为联系的桥梁.
●闯关训练
夯实基础
3.α、β是两个不重合的平面,a、b是两条不同直线,在下列条件下,可判定α∥β的是
A.α、β都平行于直线a、b
B.α内有三个不共线点到β的距离相等
C.a、b是α内两条直线,且a∥β,b∥β
D.a、b是两条异面直线且a∥α,b∥α,a∥β,b∥β
解析:A错,若a∥b,则不能断定α∥β;
B错,若A、B、C三点不在β的同一侧,则不能断定α∥β;
C错,若a∥b,则不能断定α∥β;D正确.
答案:D
2.设a、b是两条互不垂直的异面直线,过a、b分别作平面α、β,对于下面四种情况:①b∥α,②b⊥α,③α∥β,④α⊥β.其中可能的情况有
A.1种 B.2种 C.3种 D.4种
解析:①③④都有可能,②不可能,否则有b⊥a与已知矛盾.
答案:C
1.(2005年春季北京,3)下列命题中,正确的是
A.经过不同的三点有且只有一个平面
B.分别在两个平面内的两条直线一定是异面直线
C.垂直于同一个平面的两条直线是平行直线
D.垂直于同一个平面的两个平面平行
答案:C
2.两个平面平行的性质定理:如果两个平行平面都与第三个平面相交,那么交线平行.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com