2.m、n表示直线，α、β、γ表示平面，给出下列四个命题，其中正确命题为

①α∩β=m，nα，n⊥m，则α⊥β　 ②α⊥β，α∩γ=m，β∩γ=n，则m⊥n

③α⊥β，α⊥γ，β∩γ=m，则m⊥α　 ④m⊥α，n⊥β，m⊥n，则α⊥β

A.①②　　 　　　　　　　　　 B.②③　　 　　　　　　　　　 C.③④　　 　　　　　　　　　 D.②④

答案：C

1.P为△ABC所在平面外的一点，则点P在此三角形所在平面上的射影是△ABC垂心的充分必要条件是

A.PA=PB=PC

B.PA⊥BC，PB⊥AC

C.点P到△ABC三边所在直线距离相等

D.平面PAB、平面PBC、平面PAC与△ABC所在的平面所成的角相等

解析：条件A为外心的充分必要条件，条件C、D为内心或旁心的必要条件(当射影在△ABC的形内时为内心，在形外时为旁心).

答案：B

2.立体几何的计算并非单纯的数字计算，而是与作图和证明相结合的.立体几何计算题的主要步骤可以归纳为画-证-算三步.“画”是画图，添加必要的辅助线，或画出所要求的几

何量，或进行必要的转化；“证”是证明，用三段论的方法证明你所画的几何量即为所求，然后进行最后一步计算.这三步之间紧密相连，环环相扣，互相制约，形成了解决立体几何计算题的思维程序，是综合考查学科能力的集中体现.

●闯关训练

夯实基础

1.开放性问题已进入高考试卷中，近年来，全国及上海市多次考查开放题，解开放题并将经验与解题技巧相结合，并要有较熟练的基础知识和“图形意识”，并能将典型图形灵活应用到解题中去.

5.夹在互相垂直的两个平面之间长为2a的线段和这两个平面所成的角分别为45°和30°，过这条线段的两个端点分别向这两个平面的交线作垂线，则两垂足间的距离为_____________.

解析：如下图，平面α⊥β，α∩β=l，A∈α，B∈β，AB=2a.

AC⊥l于点C，BD⊥l于点D，

则CD即为所求.

∵α⊥β，AC⊥l，∴AC⊥β，∠ABC就是AB与平面β所成的角.

故∠ABC=30°，故AC=a.

同理，在Rt△ADB中求得AD=a.

在Rt△ACD，CD=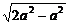=a.

答案：a

●典例剖析

[例1] 如下图，过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC⊥平面BSC.

剖析：本题是面面垂直的证明问题.一条是从定义出发的思路，即先证明其中一个平面经过另一个平面的一条垂线.但图中似乎没有现成的这样的直线，故作辅助线.根据已知条件的特点，取BC的中点O，连结AO、SO，既可证明AO⊥平面BSC，又可证明SO⊥平面ABC.另一条是从定义出发的思路，即证明两个平面所成的二面角是直二面角，注意到∠AOS是二面角A-BC-S的平面角，转化为证明∠AOS是直角.

证法一：取BC的中点O，连结AO、SO.

∵AS=BS=CS，SO⊥BC，

又∵∠ASB=∠ASC=60°，∴AB=AC，

从而AO⊥BC.

设AS=a，又∠BSC=90°，则SO=a.

又AO=== a，

∴AS²=AO²+SO²，故AO⊥OS.

从而AO⊥平面BSC，又AO平面ABC，

∴平面ABC⊥平面BSC.

证法二：同证法一证得AO⊥BC，SO⊥BC，

∴∠AOS就是二面角A-BC-S的平面角.再同证法一证得AO⊥OS，即∠AOS=90°.

∴平面ABC⊥平面BSC.

特别提示

本题揭示的是证面面垂直常用的两种方法.此外，本题中证明∠AOS=90°的方法较为特殊，即通过“算”，定量地证得直角，而不是通过位置关系定性地推理出直角，这也是立体 何中证明垂直的一种重要方法.

[例2] 如下图，在三棱锥S-ABC中，SA⊥平面ABC，平面SAB⊥平面SBC.

(1)求证：AB⊥BC；

(2)若设二面角S-BC-A为45°，SA=BC，求二面角A-SC-B的大小.

(1)证明：作AH⊥SB于H，

　∵平面SAB⊥平面SBC，

∴AH⊥平面SBC.

又SA⊥平面ABC，∴SA⊥BC.

SA在平面SBC上的射影为SH，

∴BC⊥SB.又SA∩SB=S，

∴BC⊥平面SAB.

∴BC⊥AB.

(2)解：∵SA⊥平面ABC，

∴平面SAB⊥平面ABC.又平面SAB⊥平面SBC，

∴∠SBA为二面角S-BC-A的平面角.

∴∠SBA=45°.设SA=AB=BC=a.

作AE⊥SC于E，连结EH，则EH⊥SC，∠AEH为二面角A-SC-B的平面角，

AH=a，AC=a，SC=a，AE=a，

∴sin∠AEH=，二面角A-SC-B为60°.

思考讨论

证明两个平面垂直的常见方法：

(1)根据定义，证其二面角的平面角是直角；

(2)根据判定定理，证明一个平面经过另一个平面的垂线.

[例3] 已知正三棱柱ABC-A₁B₁C₁，若过面对角线AB₁与另一面对角线BC₁平行的平面交上底面A₁B₁C₁的一边A₁C₁于点D.

(1)确定D的位置，并证明你的结论；

(2)证明：平面AB₁D⊥平面AA₁D；

(3)若AB∶AA₁=，求平面AB₁D与平面AB₁A₁所成角的大小.

剖析：本题的结论是“开放性”的，点D位置的确定如果仅凭已知条件推理难以得出.由于AB₁与BC₁这两条面对角线是相邻二侧面上的异面直线，于是可考虑将BC₁沿BA平行移动，BC₁取AE₁位置，则平面AB₁E₁一定平行BC₁，问题可以解决.

(1)解：如下图，将正三棱柱ABC-A₁B₁C₁补成一直平行六面体ABCE-A₁B₁C₁E₁，由AE₁∥BC₁，AE₁平面AB₁E₁，知BC₁∥平面AB₁E₁，故平面AB₁E₁应为所求平面，此时平面AB₁E₁交A₁C₁于点D，由平行四边形对角线互相平行性质知，D为A₁C₁的中点.

(2)证明：连结AD，从直平行六面体定义知AA₁⊥底面A₁B₁C₁D₁，且从A₁B₁C₁E₁是菱形知，B₁E₁⊥A₁C₁，据三垂线定理知，B₁E₁⊥AD.

又AD∩A₁C₁=D，所以B₁E₁⊥平面AA₁D，

又B₁E₁平面AB₁D，所以平面AB₁D⊥平面AA₁D.

(3)解：因为平面AB₁D∩平面AA₁D=AD，

所以过A₁作A₁H⊥AD于点H.

作HF⊥AB₁于点F，连结A₁F，从三垂线定理知A₁F⊥AB₁.

故∠A₁FH是二面角A₁-AB₁-D的平面角.

设侧棱AA₁=1，侧棱AB=.

于是AB₁== .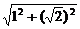

在Rt△AB₁A₁中，A₁F===，

在Rt△AA₁D中，AA₁=1，A₁D=A₁C₁=，AD== .

则A₁H==.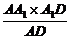

在Rt△A₁FH中，sin∠A₁FH==，

所以∠A₁FH=45°.

因此可知平面AB₁D与平面AB₁A₁所成角为45°或135°.

评述：本题主要考查棱柱的性质，以及面面关系、二面角的计算，同时考查空间想象能力和综合运用知识解决问题的能力.

特别提示

4.在正方体ABCD-A₁B₁C₁D₁中，截面A₁BD与底面ABCD所成的二面角A₁-BD-A的正切值为_____________.

答案：

3.设两个平面α、β，直线l，下列三个条件：①l⊥α；②l∥β；③α⊥β.若以其中两个作为前提，另一个作为结论，则可构成三个命题，这三个命题中正确的个数为

A.3　　　　　　　　　　　　　　　 B.2　　　　　　　　　　　　　　　 C.1　　　　　　　　　　　　　　　 D.0

解析：

答案：C

2.直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=AA₁=a，则点A到平面A₁BC的距离是

A.a　　 　　　　　　　　　　　　　　 B. a　　 　　　　　　　 C. a　　 　　　　　　 D. a

解析：取A₁C的中点O，连结AO.

　∵AC=AA₁，∴AO⊥A₁C.

又该三棱柱是直三棱柱，

∴平面A₁C⊥平面ABC.

又∵BC⊥AC，∴BC⊥AO.

因此AO⊥平面A₁BC，即A₁O等于A到平面ABC的距离.解得A₁O=a.

答案：C

1.在三棱锥A-BCD中，若AD⊥BC，BD⊥AD，△BCD是锐角三角形，那么必有

A.平面ABD⊥平面ADC　　　　　　　　　　　　　　　　　 B.平面ABD⊥平面ABC

C.平面ADC⊥平面BCD　　　　　　　　　　　　　 　　　 D.平面ABC⊥平面BCD

解析：由AD⊥BC，BD⊥ADAD⊥平面BCD，面AD平面ADC，

∴平面ADC⊥平面BCD.

答案：C

3.两个平面垂直的性质定理：如果两个平面垂直，那么过其中一个平面内的一点作它的交线的垂线与另一个平面垂直.

●点击双基